SOLUTION: If sin(x) + sin^2(x) = 1, then the value of cos^12(x) + 3cos^10(x) + 3cos^8(x) + cos^6(x) - 2 is ? (A) 0 (B) 1 (C) -1 (D) 2

Algebra ->  Trigonometry-basics -> SOLUTION: If sin(x) + sin^2(x) = 1, then the value of cos^12(x) + 3cos^10(x) + 3cos^8(x) + cos^6(x) - 2 is ? (A) 0 (B) 1 (C) -1 (D) 2      Log On


   

Question 1086313: If sin(x) + sin^2(x) = 1, then the value of cos^12(x) + 3cos^10(x) + 3cos^8(x) + cos^6(x) - 2 is ?
(A) 0
(B) 1
(C) -1
(D) 2
Found 3 solutions by ikleyn, Edwin McCravy, AnlytcPhil:
Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.


Plots y = sin%28x%29+%2B+sin%5E2%28x%29 (red) and y = 1 (green) 


1.  sin%28x%29+%2B+sin%5E2%28x%29 = 1  ====>  sin%5E2%28x%29+%2B+sin%28x%29+-1 = 0  =====>

    solve this quadratic equation for sin(x) to get a single value for sin(x) = %28-1+%2B+sqrt%285%29%29%2F2.


2.  sin%28x%29+%2B+sin%5E2%28x%29 = 1  ====>  sin(x) = 1+-+sin%5E2%28x%29 = cos%5E2%28x%29.

    Thus cos%5E2%28x%29 = %28-1+%2B+sqrt%285%29%29%2F2.


3.  cos%5E12%28x%29+%2B+3cos%5E10%28x%29+%2B+3cos%5E8%28x%29+%2B+cos%5E6%28x%29 = cos%5E6%28x%29%2A%28cos%5E6%28x%29+%2B+3%2Acos%5E4%28x%29+%2B+3%2Acos%5E2%28x%29+%2B+1%29 = cos%5E6%28x%29%2A%28cos%5E2%28x%29%2B1%29%5E3 = 

    = %28%28-1+%2B+sqrt%285%29%29%2F2%29%5E3 . %28%281+%2B+sqrt%285%29%29%2F2%29%5E3 = %28%285-1%29%2F4%29%5E3 = 1.


4.  ====>  cos%5E12%28x%29+%2B+3cos%5E10%28x%29+%2B+3cos%5E8%28x%29+%2B+cos%5E6%28x%29+-+2 = 1 - 2 = -1.


Answer. -1.

Solved.



Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
sin%28x%29+%2B+sin%5E2%28x%29+=+1

Subtracting sin2(x) from both sides,

sin%28x%29=1-sin%5E2%28x%29

Using a well-known Pythagorean identity,

sin%28x%29=cos%5E2%28x%29

Switching sides,

cos%5E2%28x%29=sin%28x%29

So, for that equation,
raising both sides to the 6th power gives cos%5E12%28x%29=sin%5E6%28x%29
raising both sides to the 5th power gives cos%5E10%28x%29=sin%5E5%28x%29
raising both sides to the 4th power gives cos%5E8%28x%29=sin%5E4%28x%29
raising both sides to the 3rd power gives cos%5E6%28x%29=sin%5E3%28x%29

So this

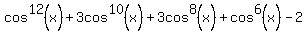cos%5E12%28x%29+%2B+3cos%5E10%28x%29+%2B+3cos%5E8%28x%29+%2B+cos%5E6%28x%29+-+2%22%22=%22%22

upon substituting those, becomes

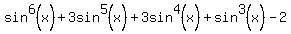sin%5E6%28x%29+%2B+3sin%5E5%28x%29+%2B+3sin%5E4%28x%29+%2B+sin%5E3%28x%29+-+2%22%22=%22%22

Factoring out sin3(x) out of the first 4 terms,

%22%22=%22%22

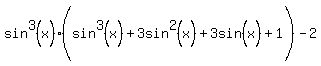Using the fact that (A+B)3 = A3+3A2B+3AB2+B3,

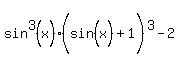sin%5E3%28x%29%28sin%5E%22%22%28x%29+%2B+1%5E%22%22%5E%22%22%29%5E3+-+2%22%22=%22%22

Writing the product of cubes as the cube of the product,

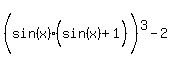%28sin%28x%29%28sin%28x%29+%2B+1%5E%22%22%29%5E%22%22%29%5E3+-+2%22%22=%22%22

Distributing,

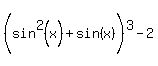%28sin%5E2%28x%29+%2B+sin%28x%29%5E%22%22%5E%22%22%29%5E3+-+2%22%22=%22%22

Reversing the terms,

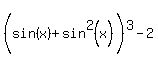%28sin%28x%29%5E%22%22%5E%22%22+%2B+sin%5E2%28x%29%29%5E3+-+2%22%22=%22%22

Notice that what's in the parentheses is exactly what is 
given as equal to 1 in the beginning, so

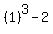
%281%29%5E3+-+2%22%22=%22%22

1-2%22%22=%22%22

-1

Edwin

Answer by AnlytcPhil(1808) About Me  (Show Source):
You can put this solution on YOUR website!
Since it's multiple choice and you don't have to understand 
anything at all as long as you get the right answer, the easy 
way is to just use your TI-83 or TI-84.  Mindlessly, follow 
this recipe:

Press Y=

Make screen read:

\Y1=sin(X)+sin(X)2
\Y2=1


Press ZOOM
Press 7
Press 2ND
Press TRACE
Press 5
Press ENTER
Press ENTER
Press ENTER
Press 2ND
Press MODE
Press CLEAR

Make the main screen read

cos(X)^12+3cos(X)^10+3cos(x)^8+cos(x)^6-2

Press ENTER

See  -1   

Edwin