SOLUTION: On 10 lbs of an alloy, there are 3 lbs of zinc, 2 lbs of copper and 5 lbs of lead. On 20 lbs of a second alloy, there are 12 lbs of zinc, 5 lbs of copper and 3 lbs of lead, while o

1-st alloy is  30% zinc,  20% copper and  50% lead.      (30% = 0.3 =  and so on . . . )

2-nd alloy is  60% zinc,  25% copper and  15% lead.      (60% = 0.6 =  and so on . . . )

3-rd alloy is  40% zink,  30% copper and  30% lead.      (40% = 0.4 =  and so on . . . )


Let x, y and z be the amounts (in lbs) of the 1-st, 2-nd and 3-rd alloy respectively to mix.


Then you need to solve this system of equations

    0.3x + 0.6y  + 0.4z = 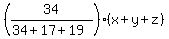,                (zink amount equation)  

    0.2x + 0.25y + 0.3z = 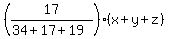,                (copper amount equation)

    0.5x + 0.15y  + 0.3z = .                (lead amount equation)


It is the first step of the setup. 
Notice that the system above is degenerated. Indeed, if you add all three equations (both sides), you will get an identity 

x + y + z = x + y + z.

It means that the solution (x,y,z) is proportional to the value (x+y+z), which is (which plays the role of) "an arbitrary parameter" in this case.
We will choose the exact final value of this parameter later to satisfy the constrains  x <= 10 lbs,  y <= 20 lbs,  z <= 20 lbs.


Now I will take this arbitrary value of parameter (x+y+z) equal to 70 = 34 + 17 + 19 (for simplicity), and will correct it later. 
With x+y+z = 70, the above system takes the form 


    0.3x + 0.6y  + 0.4z = ,     (1)

    0.2x + 0.25y + 0.3z = ,     (2)

    0.5x + 0.15y + 0.3z = .     (3)


Now apply the Cramer's rule / (the Cramer's method) to get the solution.



You may use some online solver, as I did (the popular (and free of charge) solver in this site 

https://www.algebra.com/algebra/homework/Matrices-and-determiminant/cramers-rule-3x3.solver )

to get the solution x= 20,  y= 40,  z= 10.    (4)


This solution, as I said above, is the preliminary solution.
Now I should correct it (changing all three values x= 20,  y= 40,  z= 10 proportionally) to satisfy the restrictions 
 
    x <= 10, y <= 20, z <= 20.                (5)

Reviewing/comparing these numbers (4) and (5), one can see that the solution (4) must be reduced in 2 times.


Thus the final solution is  x= 10,  y= 20  and  z= 5.