|
Question 1085997: Two boats travel in a river having a current of 5 km/hr. The boat going upstream had departed 1 hr before the boat going downstream. A period of time after the boat going downstream had departed, a radio conversation between the boats indicated that one boat was 44 km upstream and the other was 75 km downstream. Approximately, to the nearest tenth of a kilometer per hour, the speed of each boat in still water.
Find the speed of the boats in still water.
Found 2 solutions by jorel1380, ankor@dixie-net.com:
Answer by jorel1380(3719)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let r be the rate of the boats in still water (assuming they both go at the same rate). Then
44/r-5 -1=75/r+5
44(r+5) -rē+25=75(r-5)
44r+220+25-rē=75r-375
rē+31r-620=0
Using the quadratic formula, we get a positive value for r of 13.8300187521 kph for the boats in still water. ☺☺☺☺
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two boats travel in a river having a current of 5 km/hr.
The boat going upstream had departed 1 hr before the boat going downstream.
A period of time after the boat going downstream had departed, a radio conversation between the boats indicated that one boat was 44 km upstream and the other was 75 km downstream.
Approximately, to the nearest tenth of a kilometer per hour, the speed of each boat.
Find the speed of the boats in still water.
:
In order to do this problem you have to assume the boats have the same speed in still water
let s = the their still water speed
then
(s+5) = effective speed of boat1 going downstream
and
(s-5) = effective speed of boat2 going upstream
:
Write a time equation; time = dist/speed (their travel times differ by 1 hr)
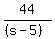 - - 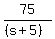 = 1 hr = 1 hr
multiply by (s-5)(s+5), cancel the denominators
44(s+5) - 75(s-5) = (s+5)(s-5)
44s + 220 - 75s + 375 = s^2 - 25
-31s + 595 = s^2 - 25
Arrange as a quadratic equation
0 = s^2 + 31s - 25 - 595
s^2 + 31s - 620 = 0
Using the quadratic formula, I got a positive solution of
s = 13.83 km/hr in still water
:
:
Check this find the actual time of boat1
75/18.83 ~ 4 hrs
find the time boat2
44/8.83 ~ 5 hrs, one hour difference
|
|
|
| |