SOLUTION: √(x+2√(x-1)) + √(x-2(√x-1))=x-1

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: √(x+2√(x-1)) + √(x-2(√x-1))=x-1      Log On


   

Question 1085982: √(x+2√(x-1)) + √(x-2(√x-1))=x-1
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
sqrt%28x%2B2sqrt%28x-1%29%29%2Bsqrt%28x-2sqrt%28x-1%29%29=x-1
If those expressions have to be defined,
it must be x-1%3E=0 .
There are too many square roots for me to write there,
so I am going to say that
y=sqrt%28x-1%29%3E=0 to make the expressions simpler.
If y=sqrt%28x-1%29 , then
y%5E2=x-1 , and y%5E2%2B1=x .
With that change of variable, the equation turns into
sqrt%28y%5E2%2B1%2B2y%29%2Bsqrt%28y%5E2%2B1-2y%29=y%5E2
sqrt%28%28y%2B1%29%5E2%29%2Bsqrt%28%28y-1%29%5E2%29=y%5E2
If y%3E=1 , then those square roots are
y%2B1%3E=2 and y-1%3E=0 .
In that case the equation simplifies to
y%2B1%2By-1=y%5E2 ,
2y=y%5E2 ,
and since y%3E=1 , we can divide both sides by y to get
2=y .
That would mean sqrt%28x-1%29=2 ,
x-1=4 , and highlight%28x=5%29 .

There is also the possibility that 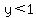y%3C1 .
In that case, 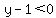y-1%3C0 , and
sqrt%28%28y-1%29%5E2%29=-%28y-1%29=1-y
From the beginning we knew that y%3E=0 ,
so 0%3C=y%3C1 ,
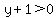y%2B1%3E0 ,
sqrt%28%28y%2B1%29%5E2%29=y%2B1 , and
the equation simplifies to
y%2B1%2B1-y=y%5E2 ,
2=y%5E2 .
However, that equation has no solutions with 0%3C=y%3C1 ,
so there are no more solutions.