Question 1085916: help me please. A Ladder tuck arrives at a high rise apartment complex where a fire has broken out.If the maximum length the ladder extends is 48ft and the angle of inclination is 45 degrees,how high up the side of the building does the ladder reach assume the ladder mounted a top a 10ft high truck. the shorter leg is 4in. Thank you.
Found 2 solutions by addingup, KMST:
Answer by addingup(3677)   (Show Source):
You can put this solution on YOUR website! You say the short leg is 4 inches? That's very unlikely. The short leg is the opposite side (opposite the hypotenuse). Let's find out:
--------------------------------
Opposite side = sin(theta) times hypotenuse;
sin(45)*48 = 33.95 feet is the length of this leg, so please check out what that 4 inches is all about.
---------------------------------
Now let's find the adjacent side (the long leg), though we already know that it's going to be the same length as the one above (see explanation below):
Adjacent side = cos(theta)*hypotenuse
= cos(45)*48 = 33.95 this is the length of this leg
--------------------------------------------
NOTE: Why are the two legs the same length? Because 1)the angles of every triangle sum 180. Since we are dealing with a right triangle, we know that one angle = 90 and if the other equals 45 the third angle must also equal 45 degrees, thus making both legs the same length.
------------------------------------------------------
How high up the side of the building?:
from the ground to the base of the ladder: 10
from the base of the ladder to the point where the ladder touches the building: 33.95
10+33.95 = 43.95 feet
-----------------------------
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! If a ladder mounted atop a 10-ft high fire truck
is extended to a length of 48 f, at an angle of  ,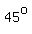
it would look like this:
 Removing the truck  ,
we just see a right triangle.
It has a  angle, of course, and two acute angles.
We are told the bottom acute angle measures ,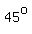
so the other acute angle measures  .
That means it is an isosceles right triangle.
In other words, the distance from the bottom of the ladder to the building wall
is the same as the vertical distance between the bottom of the ladder and the point it touches the building..
The sides of that right triangle measure, x, x, and 48ft.
Applying the Pythagorean theorem, we get
 
So, the top of the ladder is about  (or about 44 ft) above ground level.
|
|
|
