Question 1085522: A petting zoo is working to construct a rectangular pen. The pen will have 3 partitions to create separate spaces for goats,sheep,horses,and pigs.The petting zoo has 1000 feet of fencing to use.
a. Write an area function (A(x)) that gives the area of the enclosure as a function of the length of a partition, x.
b. Find the dimensions of the pen that will provide the greatest area.
c. What is the maximum area that can be enclosed?''.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A petting zoo is working to construct a rectangular pen.
The pen will have 3 partitions to create separate spaces for goats,sheep,horses,and pigs.
The petting zoo has 1000 feet of fencing to use.
a. Write an area function (A(x)) that gives the area of the enclosure as a function of the length of a partition, x.
Let L = the length, x given as the width
2L + 5x = 1000
2L = -5x + 1000
Divide both sides by 2
L = -2.5x + 500
Area
A(x) = L * x
replace L with (-2.5x+500)
A(x) = (-2.5x+500) * x
A(x) = -2.5x^2 + 500x is the function
:
b. Find the dimensions of the pen that will provide the greatest area.
Greatest area occurs on the axis of symmetry. Use x = -b/(2a)
x = 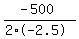
x = 100 ft is the width
Find the length
L = -2.5(100) + 500
L = -250 + 500
L = 250 ft is the length
:
c. What is the maximum area that can be enclosed?''.
250 * 100 = 25,000 sq/ft
|
|
|