SOLUTION: 4x+y=3 and (2k-1)x +(k-1)y=2k+1 is inconsistent ,find k

Algebra ->  Linear-equations -> SOLUTION: 4x+y=3 and (2k-1)x +(k-1)y=2k+1 is inconsistent ,find k      Log On


   

Question 1085335: 4x+y=3 and (2k-1)x +(k-1)y=2k+1 is inconsistent ,find k
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
For the system in the problem to be inconsistent,
the coefficients of x and y in %282k-1%29x+%2B%28k-1%29y=2k%2B1
have to equal to the coefficients in 4x%2By=3 multiplied by a certain number,
but the same cannot be true of the terms not connected to variables:
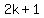2k%2B1 and 3 .
So, it must be that %282k-1%29%2F4=%28k-1%29%2F1 .
The ratio is k-1 ,
but that ratio must be different from 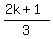%282k%2B1%29%2F3
Solving:
%282k-1%29%2F4=%28k-1%29%2F1
2k-1=4%28k-1%29
2k-1=4k-4
-1%2B4=4k-2k
3=2k
3%2F2=k
With k=3%2F2 , the coefficients' ratio is k-1=3%2F2-1=1%2F2 ,
and %282k%2B1%29%2F3=%282%28%223+%2F+2%22%29%2B1%29%2F3=%283%2B1%29%2F3=4%2F3 is not the same.
So, highlight%28k=3%2F2%29 makes the system inconsistent.

LONG-WINDED EXPLANATION:
Linear equations graph as straight lines.
If the lines intersect, there is a solution to the system:
the set of coordinates for the intersection point.
Lines that intersect do not have the same slope.
The lines could have the same slope,
as in system%284x%2By=3%2C4x%2By=5%29 , or system%284x%2By=3%2C4x%2By=3%29 , or system%284x%2By=3%2C8x%2B2y=6%29 , or system%284x%2By=3%2C8x%2B2y=10%29 .
If the slopes are the same it could be that the lines are really the same line,
as is the case with 4x%2By=3 and 8x%2B2y=6 ,
and in that case, there is an infinite number of solutions:
the sets of coordinates for each of the infinite number of points on the line.
The other possibility, if the slopes are the same is cases like system%284x%2By=3%2C4x%2By=5%29 ,
where it is obvious that the two equations cannot be true at the same time.
There are no solutions, and the system of linear equations is called inconsistent.
If 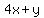4x%2By is 3 it cannot also be 5 for the same x and y values;
one equation is not consistent with the other.
Those equations represent parallel lines, with no point in common.
It is the same case with system%284x%2By=3%2C8x%2B2y=10%29 ,
although it is not so obvious. 8x%2B2y=10 is equivalent to 4x%2By=5 .
The coefficients of 8x%2B2y=10 are 2 times those of 4x%2By=3 ,
but the number 10 (not attached to any variable, on the other side of the equal sign)
is not 2 times 3.