Question 1085271: Please write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and 2,2i, 4-[6] as zeros. The brackets [] are for square roots.
Thank you!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! TIP: The conventional way to write  is sqrt(6). is sqrt(6).
1) For each real or complex zero  of a polynomial of a polynomial  , ,
there is a factor 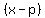 in the factorization of the polynomial. in the factorization of the polynomial.
So, if  has has  , ,  , and , and 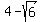 as zeros, as zeros,
the factors  , ,  , and , and  are in the factorization of are in the factorization of  . .
2) If a polynomial  has real coefficients and has a non-real complex number has real coefficients and has a non-real complex number 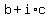 for example) as a zero, for example) as a zero,
the conjugate complex number, 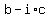 is also a zero of the polynomial, is also a zero of the polynomial,
and
if  has rational coefficients and has an irrational number such as has rational coefficients and has an irrational number such as 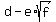 as a zero, as a zero,
the conjugate irrational number, 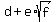 , is also a zero of the polynomial. , is also a zero of the polynomial.
In other words, irrational zeros and non-real complex zeros come as conjugate pairs.
So, along with  , ,  also has also has  as a zero, as a zero,
and along with 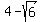 , ,  also has also has 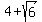 as a zero. as a zero.
Then, the factors  and and
 are also in the factorization of are also in the factorization of  . .
3) Besides at least one factor of the form 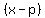 for every zero, for every zero,
the factorization of a polynomial with rational coefficients,
also has a constant factor  , which will be the leading coefficient. , which will be the leading coefficient.
So,

Simplifying,




If we really must, we multiply to get
 , and , and
 . .
|
|
|