Question 1084763: convert -2 + 0i to polar form
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! here's a pretty clear reference on how to do that.
https://www.varsitytutors.com/hotmath/hotmath_help/topics/polar-form-of-a-complex-number
i do it slightly differently, but wind up with the same answer.
my preference is to find the angle in the first quadrant and then convert it to the quadrant it is in via the following rules.
angle in second quadrant is equal to 180 minus angle in first quadrant.
angle in third quadrant is equal to 180 plus angle in first quadrant.
angle in fourth quadrant is equal to 360 minus angle in first quadrant.
conversely:
angle in first quadrant is equal to 180 minus angle in second quadrant.
angle in first quadrant is equal to angle minus 180 in third quadrant.
angle in first quadrant is equal to angle minus 360 in fourth quadrant.
i'll use that method here.
if you prefer the method in the refernece, by all means us that instead.
we have the vector in a + bi format.
this is a complex number where a represents the real part and bi represents the imaginary part.
the graph has the horizontal axis representing a and the vertical axis representing bi.
the vector is z = -2 + 0i
the size of the vector is equal to sqrt(a^2 + b^2).
in this problem, the size of the vector is therefore sqrt((-2)^2 + 0^2) = sqrt(4) = 2.
if you look at the angle formed by a and b, you will see that:
cos(theta) = a/r
sin(theta) = b/r
solve for a to get a = rcos(theta)
solve for b to get b = rsin(theta)
therefore a + bi can be represented as rcos(theta) + rsin(theta)i
factor out the r and you get a + bi = r(cos(theta) + sin(theta)i)
you find the angle by finding theta = arctan(b/a)
since b = 0 and a = -2, this becomes theta = arctan(0) which gets you theta = 0 degrees.
since 0 is right smack in the midle between first quadrant and fourth quadrant, it could be viewed as being in the first quadrant or being in the fourth quadrant.
if in the first quadrant, then it is equal to 0 degrees.
if in the fourth quadrant, then it is equal to 360 degrees.
to convert the fourth quadrant angle to the first quadrant angle, you use my rule to find that 360 minus 360 is equal to 0 in the first quadrant.
so the angle in the first quadrant is equal to 0 and, using my rule above, the equivalent angle in the second quadrant is equal to 180 minus 0 = 180.
your angle is 180 degrees.
r is equal to 2.
the polar equivalent of -2 + 0i is equal to 2 * (cos(180) + sin(180)i)
if you follow that through, then the polar equivalent of -2 + 0i is equal to 2 * (-1 + 0) which is equal to -2 + 0i.
the polar equivalent of -2 + 0i is equal to 2 * (cos(180) + sin(theta)i) and the rectangular equivalent of 2 * (cos(180) + sin(theta)i) is equal to -2 + 0i.
here's a nifty online calculator that does all the dirty work for youo.
http://www.intmath.com/complex-numbers/convert-polar-rectangular-interactive.php
i inputted -2 + 0j into the calculator and clickedon calculate and this is what it showed me.
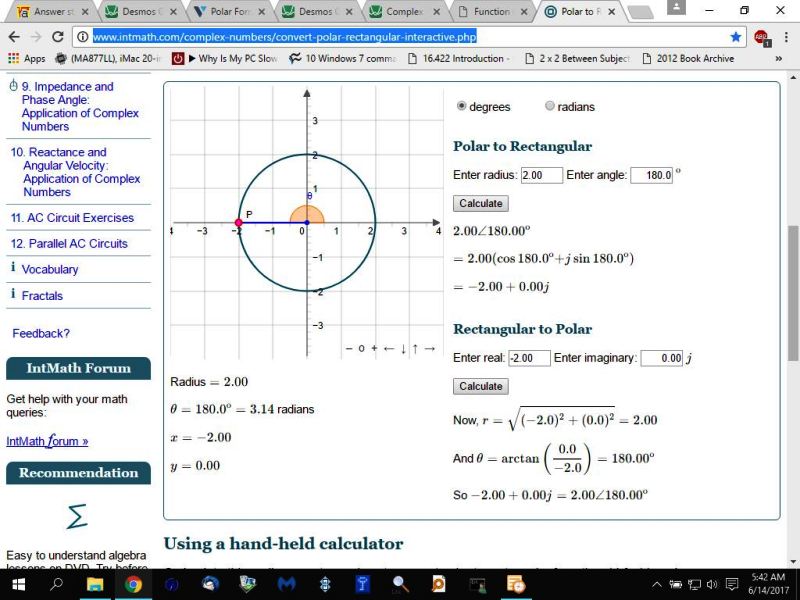
calculator appears to use j rather than i for the imaginary part.
just consider that i = j for purposes of this calculator.
also notice that = doesn't come out very clear since the bottom part of the equal sign is dark and the upper part is light so it almost looks like - rather than =.
|
|
|