|
Question 1084436: need help making sure i have the right solution for:
solve the system using determinants:
7x+3y=1
3x+4y=5
I have it reduced to 4x+ 19y= 32 is this the final answer?
Found 3 solutions by MathLover1, rothauserc, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! Determinant(D) = 7*4 - 3*3 = 19
:
D(x) = 1 * 4 - 3 * 5 = -11
:
D(y) = 7 * 5 - 1 * 3 = 32
:
x = D(x) / D = -11/19
:
y = D(y) / D = 32/19
:
**********************************
x = -11/19, y = 32/19
:
check our solution
:
7 * (-11/19) + 3 * (32/19) = 1
(-77/19) + (96/19) = 1
19/19 = 1
1 = 1
:
3 * (-11/19) + 4 * (32/19) = 5
(-33/19) + (128/19) = 5
95/19 = 5
5 = 5
:
our solution checks
***********************************
:
Answer by ikleyn(52866)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Your step is wrong and leads you to NOWHERE. For correct steps see below.
Your prerequisite is the lesson
- Solution of a linear system of two equations in two unknowns using determinant
in this site. You must know its contents in order for to understand what follows.
7x + 3y = 1
3x + 4y = 5
1. Since you need to solve it using determinants, calculate the determinant of the coefficient matrix first:
D = det 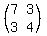 = 7*4 - 3*3 = 28 - 9 = 19.
2. To solve for the first unknown, x, you need to modify the coefficient matrix by replacing it first column by the vector/column
of the constant terms of the right side; then calculate the determinant of the modified matrix: = 7*4 - 3*3 = 28 - 9 = 19.
2. To solve for the first unknown, x, you need to modify the coefficient matrix by replacing it first column by the vector/column
of the constant terms of the right side; then calculate the determinant of the modified matrix:
 = det = det 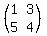 = 1*4 - 3*5 = 4 - 15 = -11.
Then the first unknown x is the ratio of the two determinants x = = 1*4 - 3*5 = 4 - 15 = -11.
Then the first unknown x is the ratio of the two determinants x = 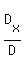 = = 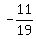 .
3. To solve for the second unknown, y, you need to modify the coefficient matrix by replacing it second column by the vector/column
of the constant terms of the right side; then calculate the determinant of the modified matrix: .
3. To solve for the second unknown, y, you need to modify the coefficient matrix by replacing it second column by the vector/column
of the constant terms of the right side; then calculate the determinant of the modified matrix:
 = det = det  = 7*5 - 1*3 = 35 - 3 = 32.
Then the second unknown, y, is the ratio of the two determinants y = = 7*5 - 1*3 = 35 - 3 = 32.
Then the second unknown, y, is the ratio of the two determinants y =  = = 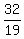 .
Answer. x = .
Answer. x = 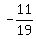 , y = , y = 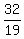 . .
Again, see the lesson.
- Solution of a linear system of two equations in two unknowns using determinant
in this site.
The lesson is the part of this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
under the topic "Systems of two linear equations in two unknowns".
Another name for the determinant method is the Cramer's rule.
On Cramer's rule for solving systems of 2 equations in 2 unknowns see the lessons
- What is a matrix?,
- Determinant of a 2x2-matrix,
- HOW TO solve system of linear equations in two unknowns using determinant (Cramer's rule),
- Solving systems of linear equations in two unknowns using the Cramer's rule,
- Solving word problems by the Cramer's rule after reducing to systems of linear equations in two unknowns,
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"2x2-Matrices, determinants, Cramer's rule for systems in two unknowns"
|
|
|
| |