Question 1084303: Find the exact values of the six trigonometric functions of θ if θ is in standard position and the terminal side of θ is in the specified quadrant and satisfies the given condition.
III; parallel to the line
7y − 2x + 4 = 0
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! it is parallel to the line 7y - 2x + 4 = 0
convert this to slope intercept form to get y = (2/7)x - 4/7
(2/7) is the slope
-4/7 is the y-intercept
the slope is 2/7 and the y-intercept is -4/7.
the equation of 7y - 2x + 4 = 0 is identical to the equation of y = (2/7)x - 4/7
the line parallel to that line has the same slope.
if it goes through the origin, then the y-intercept is 0 and the equation becomes y = (2/7)x.
since slope = the change in the value of y divided by the change in the value of x, then the triangle formed would have a vertical side length of 2 and a horizontal side length of 7.
since the tangent of the angle formed is equal to the side opposite divided by the side adjcent, then tan(theta) = 2/7.
this gets you an angle of arctan(2/7) = 15.9453959 degrees.
you can find the other functions through the use of a calculator, or you can find the length of the hypotenuse and find the other trig functions directly through their formulas.
the hypotenuse of the triangle formed is sqrt(2^2 + 7^2) = sqrt(4+49) = sqrt(53).
the sine of the angle is opp/hyp = 2/sqrt(53)
the cosine of the angle is adj/hyp = 7/sqrt(53)
the tangent of the angle is opp/adj = 2/7
the cotangent of the angle is equal to 1/tan = 7/2
the secant of the angle is 1/cos = sqrt(53)/7
the cosecant of the angle is 1/sin = sqrt(53)/2
you can use your calculator to confirm all these trig functions lead to the angle of 15.9453959 degrees.
since most calculators only do sine, cosine, and tangent, then some manipulation is required.
for example:
cot(theta) = 7/2
cot(theta) = 1/tan(theta), so 1/tan(theta) = 7/2
solve for tan(theta) to get tan(theta) = 2/7.
since tan(theta) leads to 15.9453959 degrees, you can assume cot(theta) = 7/2) is correct.
in other words, you only really need to confirm arcsin(2/sqrt(53)), arccos(7/sqrt(53)), arctan(2/7) = 15.9453959 degrees and the other trig functions will automatically be correct is you followed the rules that csc(theta) = 1/sin(theta) and sec(theta) = 1/cos(theta) and cot(theta) = 1/tan(theta).
here's a picture of your parallel line going through the origin (it's the green line).

here's a picture of the triangle formed.
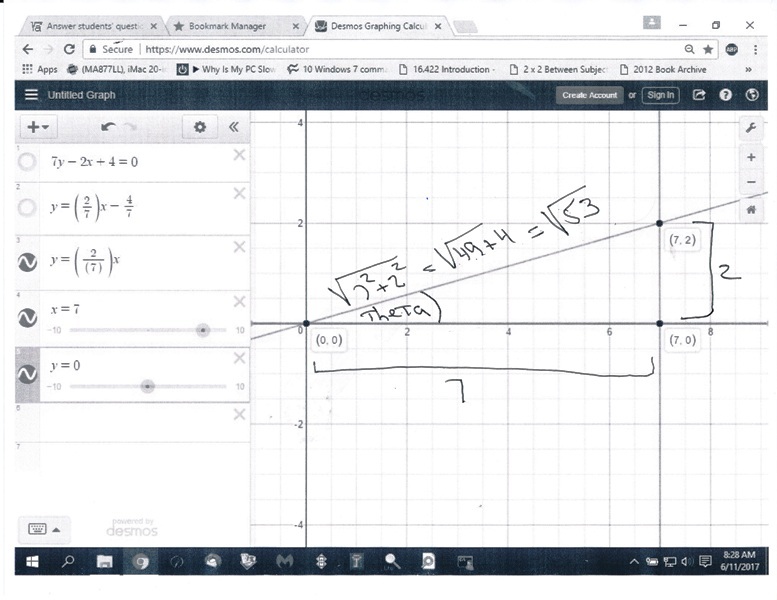
in all of the above, the terminal side of the angle was in the first quadrant.
the equivalent angle in the third quadrant would be equal to 180 + 15.9453959 degrees which would make that angle equal to 195.9453959 degrees.
in the third quadrant, sine is negative and cosine is negative and tangent is positive.
the trig functions are the same as in the first quadrant except that their sine is change.
if sine is negative, then cosecant is also negative.
if cosine is negative, then secant is also negative.
if tangent is positive, then cotangent is also positive.
here's a picture of what the triangle looks like in the third quadrant.

bottom line:
your trig functions with the angle in the third quadrant should be:
the sine of the angle is opp/hyp = -2/sqrt(53)
the cosine of the angle is adj/hyp = -7/sqrt(53)
the tangent of the angle is opp/adj = 2/7
the cotangent of the angle is equal to 1/tan = 7/2
the secant of the angle is 1/cos = -sqrt(53)/7
the cosecant of the angle is 1/sin = -sqrt(53)/2
the angle in the third quadrant is 195.9453959 degrees.
|
|
|