Question 1084278: The total number of subtractions that result in 11111 remaining after a four-digit number has been subtracted from a five-digit 1 through 9 have all been used is
Answer by math_helper(2461)   (Show Source):
You can put this solution on YOUR website! The five digit number is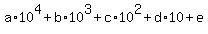 
and the four digit number is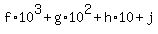 
We have:
b-f = 1
c-g = 1
d-h = 1
e-j = 1
and a = 1
Each digit of the 5-digit number is one more than the corresponding digit in the 4-digit number, and the "1" is fixed at the start of the 5-digit number.
Since all the digits 1…9 are used, the numbers must make use of the digits:
13579 and 2468, respectively
The "1" is fixed, but the 3,5,7, and 9 can be arranged in any order (that's 4! ways = 24 ways), and the 2,4,6,8 are simply re-arranged to follow along (placing 2 below 3, 6 below 7, etc., in the subtraction).
So  subtractions of a 4-digit number from a 5-digit number exist, where 1…9 are all used.
While I have not proved it rigorously, no other arrangements will give you 11111.
—
A few examples:
13579
-2468
19753
-8642
19375
-8264
etc.
|
|
|
