Question 1084203: Find p so that p+7, 3p+9, p+3,... form an arithmetic sequence
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
Find p so that p+7, 3p+9, p+3 form an arithmetic sequence
Notice that I took off ". . . " from the condition, since it MUST be so, according to the common sense.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This condition is
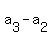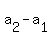 =  , or
(p+3) - (3p+9) = (3p+9) - (p+7), which implies
-2p - 6 = 2p +2,
-8 = 4p,
p = -2.
Solved.
On arithmetic progressions, see the lessons
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- Mathematical induction and arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
|
|
|
