f(x) = -2x^2 +4x + 3
Factor out the coefficient of x² out of the first two terms
on the right:
f(x) = -2(x² - 4x) + 3
1. To the side, multiply the coefficient of x inside the
parentheses by 1/2.
That's  or -1
2. Square the result of 1:
That's
or -1
2. Square the result of 1:
That's 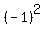 or +1
3. Add, then subtract, that inside the parentheses
f(x) = -2(x² - 2x + 1 - 1) + 3
Factor the trinomial consisting of the first three terms
inside the parentheses:
f(x) = -2((x-1)(x-1) - 1) + 3
Write (x-1)(x-1) as (x-1)²
f(x) = -2((x-1)² - 1) + 3
Remove the outer parentheses by distributing the -2 into
the outer parentheses, leaving the (x-1)² intact:
f(x) = -2(x-1)² + 2 + 3
f(x) = -2(x-1)² + 5
So the vertex is (h,k) = (1,5)
Some points besides the vertex are found by substituting
-2, -1, 0, 2, 3, 4 for x, getting:
(-2,-13), (-1,3, (0,3), (2,3), (3,-3), (4,-13)
Axis of symmetry (in green), it is x = h or, in this case,
x = 1
or +1
3. Add, then subtract, that inside the parentheses
f(x) = -2(x² - 2x + 1 - 1) + 3
Factor the trinomial consisting of the first three terms
inside the parentheses:
f(x) = -2((x-1)(x-1) - 1) + 3
Write (x-1)(x-1) as (x-1)²
f(x) = -2((x-1)² - 1) + 3
Remove the outer parentheses by distributing the -2 into
the outer parentheses, leaving the (x-1)² intact:
f(x) = -2(x-1)² + 2 + 3
f(x) = -2(x-1)² + 5
So the vertex is (h,k) = (1,5)
Some points besides the vertex are found by substituting
-2, -1, 0, 2, 3, 4 for x, getting:
(-2,-13), (-1,3, (0,3), (2,3), (3,-3), (4,-13)
Axis of symmetry (in green), it is x = h or, in this case,
x = 1
 Edwin
Edwin