Question 1084079: Given that the first 5 terms of a geometric sequence are 3, x, 12, y, and 48, find, x and y. Assume both x and y are positive.
Answer by ikleyn(52817)   (Show Source):
You can put this solution on YOUR website! .
1. Finding x.
You have these two equations
x = 3*r, (1) where "r" is unknown common ratio
12 = x*r. (2)
Substitute (1) into (2). You will get 12 = (3*r)*r or 12 = .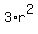
It implies  =  = 4. Hence, r = 2 or -2.
It gives two solutions for x: x = 3*2 = 6 and x = 3*(-2) = -6.
2. Finding y.
You just found that there are two possibilities for the common ratio: r = 2 and r = -2.
At the first possibility, y = 12^2 = 24.
At the second possibility, y = 12*(-2) = -24.
Answer. There are two solutions: (x,y): = (6,24) and (x,y) = (-6,-24).
Solved.
On geometric progressions, read the introductory lessons
- Geometric progressions
- The proofs of the formulas for geometric progressions
- Problems on geometric progressions
- Word problems on geometric progressions
- Solved problems on geometric progressions
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Geometric progressions".
|
|
|
