Question 1083768: Two cars are travelling on horizontal roads in straight lines, car A at
70 km/h at 800 and car B at 50 km/h at 120°. Determine the velocity
of car A relative to car B.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Two cars are travelling on horizontal roads in straight lines, car A at
70 km/h at 800 and car B at 50 km/h at 120°. Determine the velocity
of car A relative to car B.
-----------------
800 what?
Answer by ikleyn(52852)  (Show Source):
You can put this solution on YOUR website! .
Two cars are travelling on horizontal roads in straight lines, car A at
70 km/h at  80° and car B at 50 km/h at 120°.
Determine the velocity of car A relative to car B.
~~~~~~~~~~~~~~~~~~
Let O be the origin of the coordinate system O = (0,0),
OA is the segment corresponding to the location of the car A and OB be the segment corresponding to the location of the car B.
|OA| = 70*t kilometers,
|OB| = 50*t kilometers, where t is time in hours.
Apply the cosine law to determine the length of the segment AB (this length is the distance between the two cars).
Notice that the angle between OA and OB is 120° - 80° = 40°.
|AB| =  =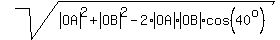
=  =
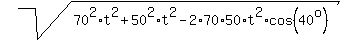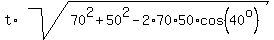=  . (1)
You see that the distance |AB| is proportional to the time.
Hence, the square root, which is the second multiplier in the formula (1), is the rate of the distance change, i.e. relative velocity,
which is under the question.
Answer. The relative velocity between the two cars is  kilometers per hour.
You do the calculations.
|
|
|
