SOLUTION: The number of sides in two regular polygons are as 5:4,and the difference between their angles is 9°;find the number of sides in the polygons.

Let n be the Greatest Common Divisor (GCD) of the numbers under the question.


Then one polygon has 5n sides, while the other has 4n sides.


It is well known fact that the sum of exterior angles of each (convex) polygon is 360 degs.


So, the exterior angle of the regular 5n-sided p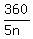olygon is .

Similarly, the exterior angle of the regular 4n-sided polygon is .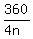


The difference between the corresponding exterior angles is 9 degs.

It gives you an equation

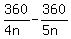 = 9,   or

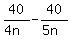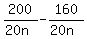 = 1,

 = 1,

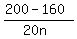 = 1,

40 = 20n  --->  n = 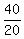 = 2.


So, the numbers of sides are 2*4 = 8 and 2*5 = 10.


Answer. The regular polygons are octagon (8 sides) and decagon (10 sides).