|
Question 1083089: The perimeter of a rectangle is 64m, what are three possible measurements for the length and width? what is the area of these rectangles?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! P = 2L + 2W
P is the perimeter
L is the length
W is the width
you can solve for L in terms of W and P as follows:
start with P = 2L + 2W
subtract 2W from both sides to get P - 2W = 2L
divide both sides fo 2 to get (P-2W)/2 = L
since you know P = 64, this becomes (64 - 2W)/2 = L
simplify to get 32 - W = L
the factors of 32 are 1, 2, 4, 8, 16, 32
W can't be 32, because then L would be 0 and that's not allowed.
if W = 16, then L = 16 and P = 2*16 + 2*16 = 32 + 32 = 64
if W = 8, then L = 24 and P = 2*8 + 2*24 = 16 + 48 = 64
if W = 4, then L = 28 and P = 2*4 + 2*28 = 8 + 56 = 64
if W = 2, then L = 30 and P = 2*2 + 2*30 = 4 + 60 = 64
if W = 1 then L = 31 and P = 2*1 + 2*31 = 2 + 62 = 64
all of these possible integer values of L and W yield P = 64.
the area, however, will be different for each one.
let A represent area.
the area of a rectangle is based on the formula of A = L * W
if W = 16, then L = 16 and A = 16 * 16 = 256
if W = 8, then L = 24 and A = 8 * 24 = 192
if W = 4, then L = 28 and A = 4 * 28 = 112
if W = 2, then L = 30 and A = 2 * 30 = 60
if W = 1 then L = 31 and A = 1 * 31 = 31
you will find that the greatest area of the rectangle is when the length and width are closest to each other in value.
this occurs when L = 16 and W = 16.
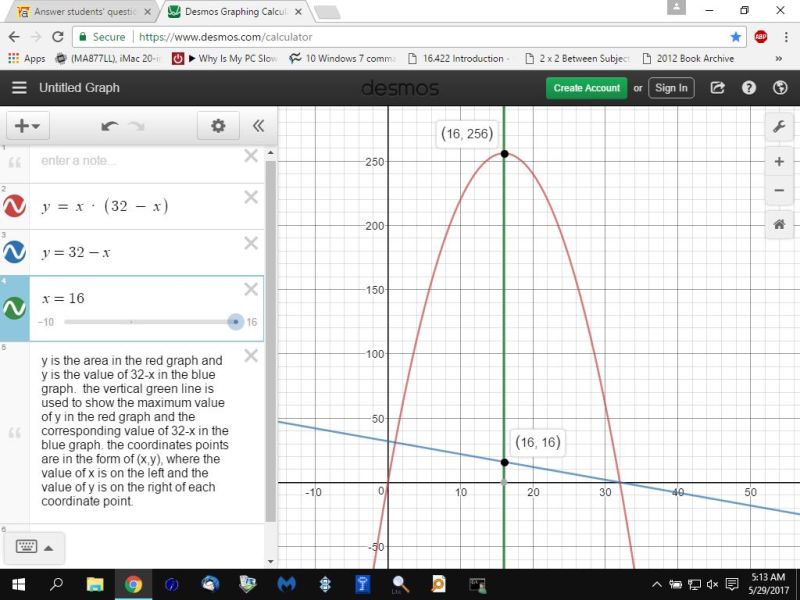
this can be seen graphically when you allow y to be the area and x to be the width.
your formula for the area becomes y = x * (32 - x)
here's what the graph looks like.
the graph of the perimeter becomes y = 2x + 2*(23-x)
here's what the graph looks like:
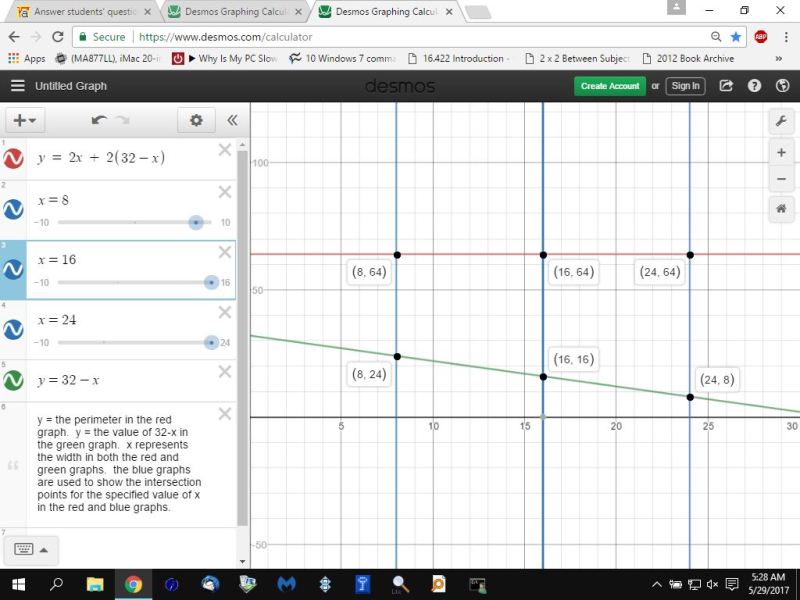
as you can see, the graph of the area forms a parabola which has a maximum value when x = (32 - x), while the graph of the perimeter is always equal to 64.
|
|
|
| |