SOLUTION: Solve the equation for 0≤x≤2pi. Write your answer as a multiple of pi if possible. sin(x)+tan(-x)=0 Thanks!

Algebra ->  Trigonometry-basics -> SOLUTION: Solve the equation for 0≤x≤2pi. Write your answer as a multiple of pi if possible. sin(x)+tan(-x)=0 Thanks!       Log On


   

Question 1082994: Solve the equation for 0≤x≤2pi. Write your answer as a multiple of pi if possible.
sin(x)+tan(-x)=0

Thanks!
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
You'll be using a few trig identities here to simplify and solve. I recommend having a sheet handy such as this one. After the first part, you'll use the unit circle to fully isolate x. The unit circle is very fundamental to trigonometry which is why it's important to have that reference sheet with you as well. Ideally you memorize everything on the sheet, but it's more practical and realistic to have the reference sheets with you.

-----------------------------------------------------------

sin%28x%29%2Btan%28-x%29=0 Start with the given equation.

sin%28x%29-tan%28x%29=0 Rewrite tan(-x) into -tan(x). This works since tangent is an odd function.

sin%28x%29-sin%28x%29%2Fcos%28x%29=0 Use the trig identity tan%28x%29=sin%28x%29%2Fcos%28x%29

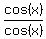sin%28x%29%2A%28cos%28x%29%2Fcos%28x%29%29-sin%28x%29%2Fcos%28x%29=0 Multiply the first sine term by cos%28x%29%2Fcos%28x%29 which is a fancy form of "1". We do this so we can have two fractions with denominator cos(x).

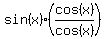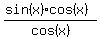
%28sin%28x%29%2Acos%28x%29%29%2Fcos%28x%29-sin%28x%29%2Fcos%28x%29=0 Rewrite sin%28x%29%2A%28cos%28x%29%2Fcos%28x%29%29 into %28sin%28x%29%2Acos%28x%29%29%2Fcos%28x%29

%28sin%28x%29%2Acos%28x%29-sin%28x%29%29%2Fcos%28x%29=0 Combine the fractions by subtracting the numerators and place that result over the common denominator.

cos%28x%29%2A%28%28sin%28x%29%2Acos%28x%29-sin%28x%29%29%2Fcos%28x%29%29=cos%28x%29%2A0 Multiply both sides by cos(x)

Notice a pair of cos(x) terms cancel on the left side...

sin%28x%29%2Acos%28x%29-sin%28x%29=0 ...which simplifies to this.

sin%28x%29%2A%28cos%28x%29-1%29=0 Factor out sin(x).

-----------------------------------------------------------

From there we use the zero product property to say

If sin%28x%29%2A%28cos%28x%29-1%29=0,

then, sin%28x%29=0 or cos%28x%29-1=0

-----------------------------------------------------------

If sin%28x%29=0, then x+=+0 or x+=+pi

Since sin%280%29=0 and sin%28pi%29=0

Use the unit circle to find these two solutions. Specifically locate the points with y coordinate of 0 and write down the corresponding angle.

Those points are (1,0) and (-1,0) corresponding to angles theta = 0 and theta = pi respectively.

-----------------------------------------------------------

If cos%28x%29-1=0, then

cos%28x%29-1=0

cos%28x%29=1

Again you'll use the unit circle, but this time you'll look for points with x coordinate of 1.

In this case, it's (1,0) which corresponds to theta = 0 and theta = 2pi.
These two angles (0 and 2pi) are coterminal. They both point directly east.

Note how cos(x) = cos(0) = 1 and how cos(x) = cos(2pi) = 1 as well.

So if cos%28x%29+=+1, then x+=+0 or x+=+2pi.

-----------------------------------------------------------

Overall, the three solutions for x, in the interval [0,2pi], are x = 0, x = pi, or x = 2pi