Question 1082960: the 3rd and 4th terms of geometric progression are 12 and 8. find the sum to infinity progression.
Found 2 solutions by KMST, amfagge92:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A geometric progression (called a geometric sequence in the USA) is a sequence of numbers (called terms) where the ratio of consecutive terms is always the same. That ratio is called the common ratio,  . .
In this case  . .
If we call the first term of our sequence  , ,
the first  terms of the progression are terms of the progression are
 , ,  , ,  , ,  , ..., , ..., 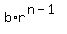 . .
The sum of those  terms is terms is
 . .
When  , ,  , so we like to write it as , so we like to write it as
 instead. instead.
In that case, as  increases, increases, 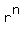 becomes smaller, becomes smaller,
tending to zero.
So the sum to infinity is  . .
In this case, the third term is
 , or , or  , or , or  . .
So,  , and the sum to infinity is , and the sum to infinity is
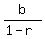 = = = =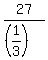 = = . .
Answer by amfagge92(93)   (Show Source): (Show Source):
You can put this solution on YOUR website! 3rd term=12
4th term=8
Nth term=ar^n-1
12=ar^2..i
8=ar^3..ii
divide through to eliminate a
3/2=r^-1
Solving i have
r=2/3
⇒12=ar^2..from i
12=a*4/3
a=27
a=27
r=2/3
S∞=a/(1-r)
=81
|
|
|