Question 108293: sketch the graph of the function. Label the vertex.
I have no idea what the vertex is
here is the problem: y=3x^2
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! The vertex is the highest or lowest point on the graph. In this case the vertex is the lowest
point. The vertex will be the lowest point if you have a quadratic equation such as this
one is AND the sign of the term that contains x^2 is a plus sign.
.
To help you a little, the graph of y = 3x^2 looks like this:
.
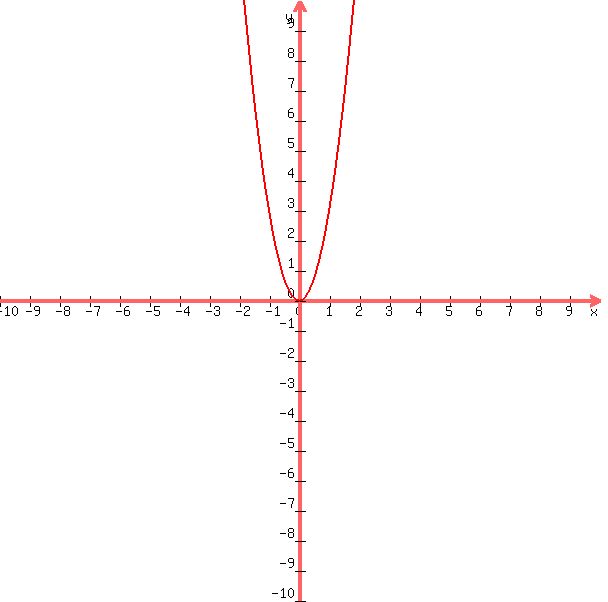
.
Notice that from this graph it looks as if the vertex is at the x, y point (0, 0),
.
If you have a quadratic equation of the form:
.
y = ax^2 + bx + c
.
The vertex will have an x value of -b/2. For this problem, since the equation you were
given has no term that contains just "x", then b must equal zero. (Similarly, there is
no constant term so "c" must also be zero. And when you compare the given equation
with the quadratic equation you can see that "a" must be 3 because the multiplier of the
x^2 term is 3.)
.
Anyhow, the vertex will occur where x has the value -b/2 and in this problem b is zero
so the vertex will occur where x = -0/2 = 0. But if x = 0, we can use the given equation to
find that:
.
y = 3x^2 = 3(0)^2 = 0.
.
Since y is zero when x is 0, we know that the vertex is at the point (0,0).
.
Hope this helps you to understand the problem and how you can find the vertex.
.
|
|
|