First you draw the triangle on graph paper:
 Then we check out each answer:
Then we check out each answer:
A. d(B;C) = 
We can just count the blocks from B to C since BC is
horizontal and find that the distance from B to C is 5,
so if it's 5, it's NOT 
B. ∠C = 90°
We can certainly see from the graph that ∠C in NOT 90°,
since it is an acute angle much smaller than 90°. It's
∠B that's 90°, not ∠C.
C. The midpoint of the hypotenuse is (-3/2, 1/2)
That's the only one left, so it must be the one that's true,
since the others are false. But let's see why anyway.
We use the midpoint formula:
Midpoint =  The hypotenuse is AC, so we substitute:
x1 = x-coordinate of A = 1
x2 = x-coordinate of C = -4
y1 = y-coordinate of A = 3
y2 = y-coordinate of C = -2
Midpoint of AC =
The hypotenuse is AC, so we substitute:
x1 = x-coordinate of A = 1
x2 = x-coordinate of C = -4
y1 = y-coordinate of A = 3
y2 = y-coordinate of C = -2
Midpoint of AC =  Midpoint of AC =
Midpoint of AC = 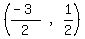 Midpoint of AC =
Midpoint of AC = 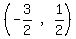 So we see this is the only one that is true.
Edwin
So we see this is the only one that is true.
Edwin