Question 1082578: How many distinct ways can the letters in the word ITEMS be arranged?
How many distinct ways can the letters in the word STEMS be arranged?
How many distinct ways can the letters in the word SEEMS be arranged?
What makes these counts different?
Found 2 solutions by ikleyn, Alan3354:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1) How many distinct ways can the letters in the word ITEMS be arranged?
2) How many distinct ways can the letters in the word STEMS be arranged?
3) How many distinct ways can the letters in the word SEEMS be arranged?
What makes these counts different?
~~~~~~~~~~~~~~~~~~~~~~~~~
1) The word ITEMS has 5 letters. They all are different (distinguishable).
Therefore, there are 5! = 5*4*3*2*1 = 120 distinct ways the letters in the word ITEMS can be arranged.
2) The word STEMS has 5 letters.
There are 4 and only 4 different (distinguishable) letters. Two letters (S) are identical.
Although there are formally 5! = 120 permutations/arrangements, not all of them are distinct/distinguishable.
Namely, in each permutation two identical letters S can be reversed in their positions, but the resulting permutations still represent the same arrangement.
Therefore, the whole number of permutations must be divided by 2 to account for this fact.
As a result, the final formula for the number of arrangements in this case is 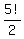 = 60.
3) The word SEEMS has 5 letters.
There are 3 and only 3 different (distinguishable) letters. There are two identical letters S and two identical letters E.
Following to the logic of the n 2), we must divide 120 (the total number of formal permutations of 5 symbols) by (2*2) = 4.
As a result, the final formula for the number of arrangements in this case is = 60.
3) The word SEEMS has 5 letters.
There are 3 and only 3 different (distinguishable) letters. There are two identical letters S and two identical letters E.
Following to the logic of the n 2), we must divide 120 (the total number of formal permutations of 5 symbols) by (2*2) = 4.
As a result, the final formula for the number of arrangements in this case is  = 30. = 30.
All question are answered. The problem is solved.
On permutations, see the lessons
- Introduction to Permutations
- PROOF of the formula on the number of Permutations
- Problems on Permutations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! How many distinct ways can the letters in the word ITEMS be arranged?
5! = 120, as the other tutor stated.
---
How many distinct ways can the letters in the word STEMS be arranged?
5!/2 = 60.
It's divided by 2 because 2 letters are the same.
---
How many distinct ways can the letters in the word SEEMS be arranged?
5!/4 = 30
It'd divided by 2 twice because there are 2 duplicate letters.
|
|
|