SOLUTION: Find k when (x-4) is a factor of 2x^2-3x+k

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Find k when (x-4) is a factor of 2x^2-3x+k      Log On


   

Question 1082514: Find k when (x-4) is a factor of 2x^2-3x+k
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39628) About Me  (Show Source):
You can put this solution on YOUR website!
Root of 4, remainder must be 0. 

Synthetic Division for root of 4:

4    |    2    -3    k
     |
     |         8    20
     |_________________________
         2     5    k+20

k%2B20=0
highlight%28k=-20%29

Answer by ikleyn(52866) About Me  (Show Source):
You can put this solution on YOUR website!
.
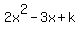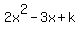The fact that (x-4) is a factor of 2x%5E2-3x%2Bk is equivalent, due to the Remainder theorem, that x= 4 is the root 
of the polynomial p(x) = 2x%5E2-3x%2Bk, i.e. P(4) = 0,  or

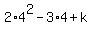    2%2A4%5E2+-+3%2A4+%2B+k = 0.


It implies 

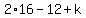    2%2A16+-+12+%2B+k+ = 0,  or  32 - 12 + k = 0  --->  k = -20.


Answer.   k = -20.


On the Remainder theorem see the lesson Divisibility of polynomial f(x) by binomial x-a in this site.


---------------------
    The remainder theorem

    1. The remainder of division the polynomial  f%28x%29  by the binomial  x-a  is equal to the value  f%28a%29  of the polynomial. 

    2. The binomial  x-a  divides the polynomial  f%28x%29  if and only if the value of  a  is the root of the polynomial  f%28x%29,  i.e.  f%28a%29+=+0.

    3. The binomial  x-a  factors the polynomial  f%28x%29  if and only if the value of  a  is the root of the polynomial  f%28x%29,  i.e.  f%28a%29+=+0.
---------------------


Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic
"Divisibility of polynomial f(x) by binomial (x-a). The Remainder theorem".