Question 1082339: Find the locus of points P(x,y) such that the distance from P to (3,0) is twice its distance to (1,0).
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39618)   (Show Source):
Answer by ikleyn(52797)  (Show Source):
You can put this solution on YOUR website! .
Find the locus of points P(x,y) such that the distance from P to (3,0) is twice its distance to (1,0).
~~~~~~~~~~~~~~~~~~
Let (x,y) be the point of this locus.
Then
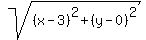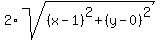 =  . (1)
The left side is the distance from (x,y) to the point (3,0).
The right side is the doubled distance from (x,y) to the point (1,0).
Now square both sides of (1). You will get
 =  .
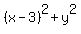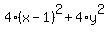Simplify:
 =  ,
 =  ,
 =  ,
 =  ,
 =  ,
=  .
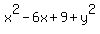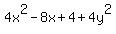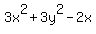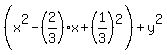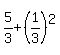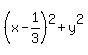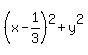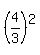It is the equation of the circle of the radius  with the center at the point ( , ).
Answer. The locus under the question is the circle of the radius with the center at the point (,).
Circle =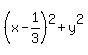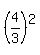
|
|
|
