Question 1082067: In forming 5 letter words using the letters of the word EQUATIONS. Note that a word is an ordered arrangement of letters. How many
(i) consist only of vowels?
(ii) contain all the consonants?
(iii) begin with an ‘T’ and end in ‘Q’? (iv) begin with a consonant?
(v) contain ‘S’?
(vi) in which the vowels and consonants alternate?
(vii) in which ‘Q’ is immediately fo
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! IF LETTERS CAN BE REPEATED,
AAAAA could be considered a word.
Then, a lot more words could be formed.
(i) You have 5 options for each of the 5 letters,
so you can form  5-letter words.
(ii) There would be the 4 consonants,
arranged in any of  different orders,
plus an additional letter.
Of the additional letter chosen is a vowel,
there are 5 letter choices and 5 position choices.
That would yield  words including all consonants and a vowel.
Choosing one of the 4 consonants as the additional letter,
would yield 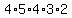 different arrangements IF
we could distinguish the added consonsnt
from the one just like it in the 4 arranged first.
Since they cannot be distinguished,
the number of different arrangements of 5 vowels formed would be only
 .
So the number of 5-letter words (repetition allowed)
containing all 4 consonants would be
 .
(iii) If the 5-letter word must begin with a certain letter,
and send with another letter,
there are  arrangements of all 9 letters
that could be used to fill the 3 positions in between.
IF LETTERS CANNOT BE REPEATED:
(i) There are  permutations of 5 different vowels.
(ii) There are only  consonants in the word EQUATIONS, so to make a 5-letter word, with all 4 consonants, and no repeated letters, a vowel would have to be included .
With  possible permutations of the consonants,
 choices for the vowel to include, and
positions to place the chosen vowel,
there are possible words.
Calculating it a different way,
You could make different sets of 5 letters including all consonants and 1 vowel.
For each of those sets,
there are ways to arrange them,
making  5-letter words.
(iii) If those two letters are preselected for first and last letter,
there are  lettered to choose the 3 middle letters from.
That gives us  choices.
(iv) There are choirs of consonant for the first letter.
There are  choices for the sequence of 4 different letters to follow.
So, there are  5-letter words
starting with s consonant, with no repeated letters.
(v) Using all 9 letters,
There are {9!=9*8*7*6*5}}} 5-letter words that can need formed with no repeated letters.
Excluding S, you could only form
{8!=8*7*6*5*4}}} .
So, there are
words containing S.
(vi) If you want vowels and consonants to alternate,
you can start with a vowel or a consonant.
If you start with a vowel, you will use 3 vowels,
in one of 
different arrangements.
You will have  possible arrangements of 2 different consonants to fill the 2nd and 4th letter positions.
That makes  different words alternating voweks and consonants, staring with a vowel.
Starting with a consonant,
you would have  different arrangements of 3 consonants,
and  different arrangements of 3 vowels,
For a total of  5-letter words,
alternating vowels and consonants starting with a consonant.
In all, you would have  5-letter words alternating vowels and consonants.
|
|
|
