|
Question 1081946: Find equation when the center on the line x - 2y - 9 = 0 and passes through the points (7,-2) and (5,0).
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find equation when the center on the line x - 2y - 9 = 0 and passes through the points (7,-2) and (5,0).
~~~~~~~~~~~~~~~~~~~~
The center of the circle lies on the perpendicular bisector to the segment connecting the points (7,-2) and (5,0).
The midpoint is (6,-1). (6 = 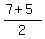 , -1 = , -1 = 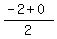 )
The segment connecting the given points has the slope )
The segment connecting the given points has the slope 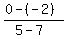 = = 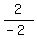 = -1.
Therefore, the perpendicular bisector has the slope 1.
Hence, the perpendicular bisector passing through the point (6,-1) has the equation
y - (-1) = 1*(x-6), or, which is the same, y+1 = x - 6.
Hence, the center of the circle lies at the intersection of these two lines
x - 2y - 9 = 0 (1) and
y+1 = x - 6. (2)
This system is the same as
x - 2y = 9, (3)
x - y = 7. (4)
To solve the system (and to find the intersection point) subtract (4) from (3) both sides). You will get
-y = 2, or y = -2.
Then x = 7 + y = 7 + (-2) = 5 (from (4).
Thus the point (5,-2) is the center.
The distance from the center (5,-2) to the given point (5,0) is = -1.
Therefore, the perpendicular bisector has the slope 1.
Hence, the perpendicular bisector passing through the point (6,-1) has the equation
y - (-1) = 1*(x-6), or, which is the same, y+1 = x - 6.
Hence, the center of the circle lies at the intersection of these two lines
x - 2y - 9 = 0 (1) and
y+1 = x - 6. (2)
This system is the same as
x - 2y = 9, (3)
x - y = 7. (4)
To solve the system (and to find the intersection point) subtract (4) from (3) both sides). You will get
-y = 2, or y = -2.
Then x = 7 + y = 7 + (-2) = 5 (from (4).
Thus the point (5,-2) is the center.
The distance from the center (5,-2) to the given point (5,0) is 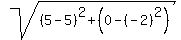 = = 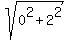 = =  = 2.
Then the equation of the circle is = 2.
Then the equation of the circle is
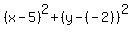 = 4, or = 4, or
 = 4. = 4.
Solved.

The solution by "josgarithmetic" is WRONG.
|
|
|
| |