|
Question 1081944: 80 men can finish the job in 60 days. At the 16th day, 5 men were laid off and at the 45th day, 10 men were hired. How many days were they delayed finishing the job.
Found 2 solutions by josmiceli, Theo:
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! 80 men can finish the job in 60 days.
So, the rate of working for 80 men is:
[ 1 job ] / [ 60 days ]
The rate for 1 man is only 1/80 of that, so
the rate of working for 1 man is:
[ 1 job ] / [ 4800 days ] = 
-----------------------------------------
Did they only get 15 days out of the 80 men?
If that's so, then, they finished
 of the job in 15 days, so
there is  of the job left to do
------------------------------------------
Fom the 16 day to the 44th day is 29 days
There are  men working for
29 days, so they can do:
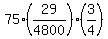 of the 3/4 job left to do
so they do this fraction of the job:
---------------------------------
So far,  of the job is done
 is done, so
that leaves 
of the job left to do
-------------------------
10 men were hired, so there are  men
Let  = days it takes to do the fraction of the job left
----------------------
Adding up the days:
 days to finish job
They were delayed 7.16 days
----------------------------
Definitely get another opinion on this, and
check my math carefully. I could be off on
exactly how long each man worked.
Hope this helps.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! the formula to use is:
p * r * t = q
p is the number of people working.
r is the rate that each person works at.
t is the time.
q is the quantity of work.
in your problem:
p = 80
r = something you have to find.
t is 60 days
q is 1 job.
the formula becomes 80 * r * 60 = 1
solve for r to get r = 1/4800.
each person works at the rate of 1/4800 of the job each day.
the assumption is that all of the people work at the same average rate, which doesn't change.
on the 16th day, 5 men were laid off.
this means 80 men were working from day 1 to day 15.
on the 45th day, 10 men were hired.
this means that 75 men were working from day 16 to day 44, and that 85 men were working from day 45 to day 60.
we have 15 days when 80 men were working.
we have 29 days when 75 men were working.
we have 16 days when 10 men were working.
80 * 1/4800 * 15 + 75 * 1/4800 * 29 + 85 * 1/4800 * 16 = .9864583333
this means that .9864583333 of the job was finished in 60 days.
since 85 men were still working at the rate of 1/4800 of the job per mean per day, then the 85 men were working at the rate of 85/4800 of the job each day.
they still have (1 - .9864583333) of the job to go.
that means that they still had .0135416667 of the job to go.
divide that by 85/4800 and you get .7647058824 days to go.
add that to the number of days 85 men were working and the formula becomes:
80 * 1/4800 * 15 + 75 * 1/4800 * 29 + 85 * 1/4800 * 16.7647058824 = 1
looks like they were delayed a little more than 3/4 of a day.
a slightly different way of looking at this that should give you the same answer would be:
80 * 1/4800 * 15 = .25 of the job.
75 * 1/4800 * 29 = .453125 of the job.
the amount of the job that 85 men have to finish is equal to .296875 of the job.
85 * 1/4800 * t = .296875
solve for t to get t = .296875 * 4800 / 85 = 16.76470588
15 + 29 + 16.76470588 is equal to 60.76470588 days which is .76470588 days more than the original 60 days that were planned.
if you round it to the nearest day, then they were 1 day late.
that's my take.
the assumption here is that the 85 men were there until the job was finished.
|
|
|
| |
