Question 1081854: Given the polynomial f(x)= x^4 -6x^3 +9x^2 +4x -12 ,
(I) factorize f(x) completely and hence find the x and y axes intercepts
(II) state the x coordinates where the graph of y=f(x) cuts the x-axis and where it touches the x-axis
(III) draw a sign diagram for f(x)
(IV) discuss the behaviour of f(x) as x = ∞ and as x = -∞
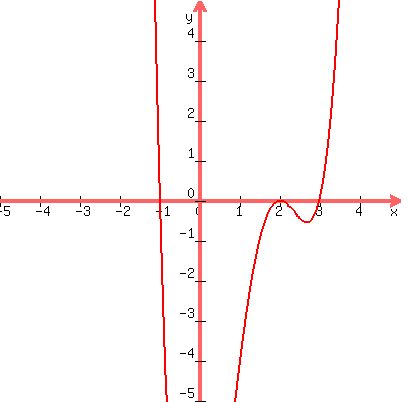
(V) sketch the graph of y=f(x), using the information obtained above.
Answer by josgarithmetic(39626)   (Show Source): (Show Source):
You can put this solution on YOUR website! Possible roots to try would be -6,-4,-3,-2,-1,1,2,3,4,6,12 (Rational Roots Theorem).
2 | 1 -6 9 4 -12
| 2 -8 2 12
|________________________________
1 -4 1 6 0
3 | 1 -4 1 6
|
| 3 -3 -6
|______________________________
1 -1 -2 0
Partial factorizing gives  . .
The quadratic factor breaks into f being


x-intercepts:
-1, 2, 3
y-intercept:
When x=0, y=-12.
Table of Signs:
Check inside each interval on x.
-
(infin, -1]
[-1, 2]
[2, 3]
[3, infinity)
-
You can determine the result in each interval on your own.


|
|
|