SOLUTION: How many ordered pairs of integers (x, y) satisfy y^2 - xy + x = 0?

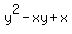
Solve for x







,  

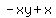
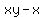
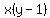
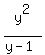By synthetic division, divide y2+0y+0 by y-1

1 | 1 0 0
  |   1 1
    1 1 1



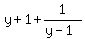Since x and y must be integers, so must ,

and so the denominator y-1 must be 1 or -1.

If the denominator = 1

y-1 = 1
  y = 2



So one ordered pair is (x,y) = (4,2)

If the denominator = -1

y-1 = -1
  y = 0



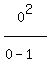
So the only other ordered pair is (x,y) = (0,0) 

So there are two ordered pairs that satisfy the given equation.

Edwin