SOLUTION: Prove that {{{ n^3 + 5n }}} is divisible by 6, where n is any positive integer.

Algebra ->  Divisibility and Prime Numbers -> SOLUTION: Prove that {{{ n^3 + 5n }}} is divisible by 6, where n is any positive integer.      Log On


   

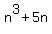Question 1081675: Prove that +n%5E3+%2B+5n+ is divisible by 6, where n is any positive integer.
Answer by ikleyn(52817) About Me  (Show Source):
You can put this solution on YOUR website!
.
Prove that +n%5E3+%2B+5n+ is divisible by 6, where n is any positive integer.
~~~~~~~~~~~~~~~~

My proof consists of two parts.

Part 1. For any integer n, 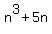+n%5E3+%2B+5n+ is divisible by 2. 
    Consider consequently the case of even "n" and the case of odd "n".
    In both cases, the statement is true, which is OBVIOUS.

Part 2. For any integer n, 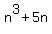+n%5E3+%2B+5n+ is divisible by 3. 
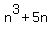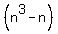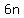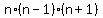    n%5E3+%2B+5n = %28n%5E3-n%29 + 6n = n%2A%28n-1%29%2A%28n%2B1%29 + 6n.


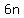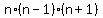    n%2A%28n-1%29%2A%28n%2B1%29 is always multiple of 3, since it is the product of three consecutive integers.

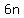    6n is always multiple of 3, by the obvious reason.

    So the statement of the Part 2 is proven, too.

Thus the general statement follows regarding divisibility by 6.