Question 1081571: Write the equation of a hyperbola with foci at (3, -3) and (3, 7) and vertices at (3, -1) and (3, 5).
Write the equation of a hyperbola with vertices (0, -4) and (0, 4) and foci (0, -5) and (0, 5).
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Write the equation of a hyperbola with foci at ( , ,  ) and ( ) and ( , ,  ) and vertices at ( ) and vertices at ( , ,  ) and ( ) and ( , , ). ).
determine if it is
horizontal: 
or
vertical: 
To start, let's graph the information we have:

so,you have vertical:

now
1. Identify the center point ( , ,  ) )
it is midpoint of line segment:( , ,  ) and ( ) and ( , ,  ) )
(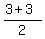 , , 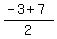 )=( )=( , ,  ) )
The center point is ( , ,  )=( )=( , ,  ). ).
so, and and 
put it on a graph:

2. Identify  and and 
To find  , we'll count from the center to either vertex; , we'll count from the center to either vertex;  . .
To find  , we'll count from the center to either focus; , we'll count from the center to either focus;
3. Use the formula  to find to find  (or (or  ) )



 -> ->
4. Plug  , ,  , ,  , and , and  into the correct pattern. into the correct pattern.



next problem is of same type; so,I am pretty sure you can do it following these steps
|
|
|