.
A circle is tangent to both the X and Y axes and is tangent to the line 3x+4y=60 at the point (8,9). Find the equation.
~~~~~~~~~~~~~~~~~~~~~~
Since the "circle is tangent to both the X and Y axes", its center lies on the line y = x OR on the line y = -x.
Since the circle "is tangent to the line 3x+4y=60 at the point point (8,9)", its center lies on the perpendicular to the given line
at the given point.
The given line has the slope  , hence, the perpendicular line has the slope of
, hence, the perpendicular line has the slope of  .
Then the equation of this perpendicular line through the given (8,9) is
y-9 =
.
Then the equation of this perpendicular line through the given (8,9) is
y-9 = 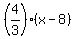 (2)
So, the center of the circle is EITHER the intersection of two straight lines
y = x, y-9 =
(2)
So, the center of the circle is EITHER the intersection of two straight lines
y = x, y-9 = 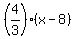 , (3)
OR is the intersection of two straight lines
y = -x, y-9 =
, (3)
OR is the intersection of two straight lines
y = -x, y-9 = 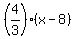 , (4)
Case 1. y = x, y-9 =
, (4)
Case 1. y = x, y-9 = 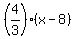 (3) ====> (simply replace y by x in the left part of the second equation) ====>
x - 9 =
(3) ====> (simply replace y by x in the left part of the second equation) ====>
x - 9 = 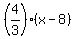 ====> 3x - 27 = 4x - 32 ====> x = 5.
Then y = 5, and the center in this case is the point (x,y) = (5,5).
Then the radius of the circle = the distance from the center to the point (8,9) =
====> 3x - 27 = 4x - 32 ====> x = 5.
Then y = 5, and the center in this case is the point (x,y) = (5,5).
Then the radius of the circle = the distance from the center to the point (8,9) =  = 5.
It is consistent with the fact that the circle touches the x-axis and y-axis.
Case 2. y = -x, y-9 =
= 5.
It is consistent with the fact that the circle touches the x-axis and y-axis.
Case 2. y = -x, y-9 = 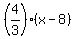 (4) ====> (simply replace y by -x in the left part of the second equation) ====>
-x - 9 =
(4) ====> (simply replace y by -x in the left part of the second equation) ====>
-x - 9 = 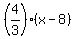 ====> -3x - 27 = 4x - 32 ====> 7x = 5 ====> x =
====> -3x - 27 = 4x - 32 ====> 7x = 5 ====> x =  .
Then y =
.
Then y =  , and the center in this case is the point (x,y) = (
, and the center in this case is the point (x,y) = ( ,
, ).
Then the radius of the circle = the distance from the center to the point (8,9) =
).
Then the radius of the circle = the distance from the center to the point (8,9) =  .
Clearly/obviously, it is NOT consistent with the fact that the circle touches the x-axis and y-axis.
So, the center of the circle is UNIQUELY defined at (5,5) and the radius of the circle is 5.
Thus the equation of the circle is
.
Clearly/obviously, it is NOT consistent with the fact that the circle touches the x-axis and y-axis.
So, the center of the circle is UNIQUELY defined at (5,5) and the radius of the circle is 5.
Thus the equation of the circle is 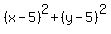 = 5.
= 5.
Solved.