SOLUTION: Find the point whose distance from (7, -3) is √58 and whose abscissa equals its ordinate. Find the coordinates of the point equidistant from (1, -6), (5, -6) and (6, -1).

Algebra ->  Length-and-distance -> SOLUTION: Find the point whose distance from (7, -3) is √58 and whose abscissa equals its ordinate. Find the coordinates of the point equidistant from (1, -6), (5, -6) and (6, -1).      Log On


   

Question 1081097: Find the point whose distance from (7, -3) is √58 and whose abscissa equals its ordinate.
Find the coordinates of the point equidistant from (1, -6), (5, -6) and (6, -1).
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
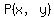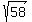
The point P%28x%2Cy%29 whose distance from (7, -3) is sqrt%2858%29
is part of the circle with equation
%28x-7%29%5E2%2B%28y%2B3%29%5E2=58 .
The point 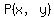P%28x%2Cy%29 whose abscissa equals its ordinate has x=y .
(The equation x=y is the equation of a line).
Substituting x for y in the first equation, we get
%28x-7%29%5E2%2B%28x%2B3%29%5E2=58 .
We can simplify and solve:
x%5E2-14x%2B49%2Bx%5E2%2B6x%2B9=58
2x%5E2-8x%2B58=58
2x%5E2-8x=0
2x%28x-4%29=0
That last equation's solutions are
x=0 and x=4 .
So, the points whose distance from (7, -3) is 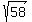sqrt%2858%29 ,
and whose abscissa equals its ordinate are highlight%28P%280%2C0%29%29 and highlight%28Q%284%2C4%29%29 .


The points equidistant from 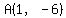A%281%2C+-6%29 and B%285%2C+-6%29 are
on the perpendicular bisector of AB. and (6, -1).
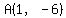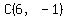The points equidistant from A%281%2C+-6%29 and C%286%2C-1%29 are
on the perpendicular bisector of AC.
We can find the equations for those two lines.
The point equidistant form A, B, and C is in the intersection of those two lines.
Segment AB is a "horizontal" segment (part of the y=-6 line),
with midpoint 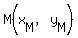M%28x%5BM%5D%2Cy%5BM%5D%29 , with x%5BM%5D=%28x%5BA%5D%2Bx%5BB%5D%29%2F2=%281%2B5%29%2F2=3.
Its perpendicular bisector is the "vertical" line, passing through M,
and that is the line represented by x=3 .
Segment AC is part of a line with slope

The midpoint of segment AC, 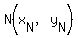N%28x%5BN%5D%2Cy%5BN%5D%29 , has coordinates
x%5BN%5D=%28x%5BA%5D%2Bx%5BC%5D%29%2F2=%281%2B6%29%2F2=7%2F2=3.5 and
y%5BN%5D=%28y%5BA%5D%2By%5BC%5D%29%2F2=%28-6%2B%28-1%29%29%2F2=%28-7%29%2F2=-7%2F2=-3.5 .
The perpendicular bisector of AC has slope %28-1%29%2Fm%5BAC%5D=%28-1%29%2F1=-1 ,
and passes through 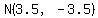N%283.5%2C-3.5%29 , so its equation is
y-%28-3.5%29=%28-1%29%28x-3.5%29 --> y%2B3.5=-x%2B3.5 --> y=-x .
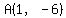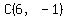
The point equidistant from A%281%2C+-6%29 , B%285%2C+-6%29 and C%286%2C-1%29
can be found from
system%28x=3%2Cy=-x%29 --> system%28x=3%2Cy=-3%29 .
So, the point equidistant from A, B, and C is 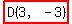highlight%28D%283%2C-3%29%29 .


MORE: Let's say you want to find a point 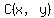C%28x%2Cy%29 that is at a distance 4sqrt%282%29 from A%28-3%2F2%2C+-5%2F2%29=A%28-1.5%2C-2.5%29 , and at a distance 2sqrt%285%29 from B%289%2F2%2C-5%2F2%29=B%284.5%2C-2.5%29
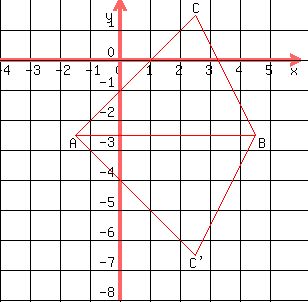
You could draw AB, and use a compass to draw arcs (or circles) centered at A and B,using the given distances as radii, and find the location of point C where the arcs (or circles) intersect.
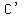You would realize that there are two solutions: C and its mirror image, %22C+%27%22 .
You could sketch the triangle ABC; draw the altitude from C to AB, and then apply the Pythagorean theorem to the right triangles formed, to find the location for point C.

You could apply the distance formula.
When trying to get the coordinates of point C, all those approaches end in the same equations,
because the distance formula and the equation of a circle are both derived from the Pythagorean theorem.
The equations you end up with are:
%28x-%28-1.5%29%29%5E2%2B%28y-%28-2.5%29%29%5E2=%284sqrt%282%29%29%5E2 --> %28x%2B1.5%29%5E2%2B%28y%2B2.5%29%5E2=32
%28x-4.5%29%5E2%2B%28y-%28-2.5%29%29%5E2=%282sqrt%285%29%29%5E2 --> %28x-4.5%29%5E2%2B%28y%2B2.5%29%5E2=20
Subtracting one equation from the other, we get
%28x%2B1.5%29%5E2-%28x-4.5%29%5E2=32-12
%28%28x%2B1.5%29%2B%28x-4.5%29%29%2A%28%28x%2B1.5%29-%28x-4.5%29%29=12
%28x%2B1.5%2Bx-4.5%29%2A%28x%2B1.5-x%2B4.5%29=12
%282x-3%29%2A6=12
2x-3=2
2x=5
highlight%28x=5%2F2=2.5%29
Substituting that value into either of the original equations, we find to values for y .
%282.5%2B1.5%29%5E2%2B%28y%2B2.5%29%5E2=32
4%5E2%2B%28y%2B2.5%29%5E2=32
16%2B%28y%2B2.5%29%5E2=32
%28y%2B2.5%29%5E2=16
y%2B2.5=%22+%22+%2B-+4 --> y=-2.5+%2B-+4 --> highlight%28system%28y%5B%22C+%27%22%5D=-6.5%2Cy%5BC%5D=1.5%29%29