.
If tan(x) + cot(x) = 2, then
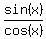 +
+ 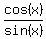 = 2, ---->
= 2, ---->
 +
+  = 2, ---->
= 2, ---->
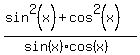 = 2, ---->
= 2, ---->
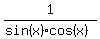 = 2,
2sin(x)*cos(x) = 1 ---> sin(2x) = 1 ---> 2x =
= 2,
2sin(x)*cos(x) = 1 ---> sin(2x) = 1 ---> 2x =  ---> x =
---> x =  or x =
or x =  .
In any case, tan(x) = 1 and cot(x) = 1.
So, we proved that if tan(x) + cot(x) = 2 then tan(x) = 1 and cot(x) = 1.
2. Having this, you have
.
In any case, tan(x) = 1 and cot(x) = 1.
So, we proved that if tan(x) + cot(x) = 2 then tan(x) = 1 and cot(x) = 1.
2. Having this, you have  =
= 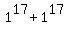 = 1 + 1 = 2.
= 1 + 1 = 2.
Answer. if tan(x) + cot(x) = 2 then  = 2.
= 2.
Solved.