SOLUTION: Please help me solve this problem: If xy = 64 and {{{ log (x, y) + log (y, x) = 5/2 }}} find x and y.

 = .      (1)

Well known rule for the base change of logarithms says that   = .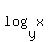

Therefore, the equation (1) becomes

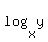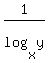 +  = .   (2)

To solve it, introduce new variable  z = 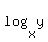.  Then the equation (2) becomes

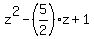 = ,   or    = 0,   or 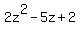   = 0.

Use the quadratic formula to find its roots. The roots are   = 2   and/or   = .


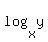1.   = 2  ====>   = 2  ====>  y = x^2. 

    Substitute it into the equation  xy = 64,  and you will get   = 64,   which implies  x = 4.

    In this case, the solution of the original system is  x = 4,  y = 16.


2.   =   ====> 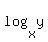  =   ====>  y = x^(1/2). 

    Substitute it into the equation  xy = 64,  and you will get  x^(3/2) = 64,   which implies   = 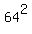  and hence  x = 16.

    In this case, the solution of the original system is  x = 16,  y = 4.