SOLUTION: Two cars A and B are to race around a 1500-meter circular track. If they will start at the same point and travel opposite directions, they will meet for the first time in 3 minutes

Let "a" be the rate of the car A (in meters-per-minute), and
let "b" be the rate of the car B.

Then you have these two equations for two unknowns "a" and "b":

3a + 3b = 1500.     (1)      ("If they will start at the same point and travel opposite directions, 
                               they will meet for the first time in 3 minutes.")

 = 1000     (2)      ("But if they travel in the same direction, with the same starting point, 
                               car A will reach the starting point with car B traveling behind by 500 meters")


Equation (1) is clear and does not require further explanation: the two cars, moving towards each other, 
cover exactly one lap of 1500 meters long.

The equation (2) requires some explanations:

    a) The factor 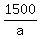 is the time for car A to reach the starting point;
    b) Car B traveled that time 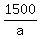 and covered only 1500 - 500 = 1000 meters.

    Thus equation (2) is simply the "distance" equation D = R*T for the car B.

OK. Let us simplify equations (1) and (2):

a + b = 500      (1')    ( 500 =  )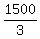
3b = 2a          (2')    ( after cross-multiplication and canceling in equation (2) )


To solve it, express a = 500 -b from (1') and substitute it into (2') to get

3b = 2(500-b)  --->  3b = 1000 - 2b  --->  b = 200 m/minute

--->  a = 300 m/minute.