Question 1079572: Two cars A and B are to race around a 1500-meter circular track. If they will start at the same point and travel opposite directions, they will meet for the first time in 3 minutes. But if they travel in the same direction, with the same starting point, car A will reach the starting point with car B trailing behind by 500 meters. What should be the rate of car A and car B?
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two cars A and B are to race around a 1500-meter circular track.
If they will start at the same point and travel opposite directions, they will meet for the first time in 3 minutes.
But if they travel in the same direction, with the same starting point, car A will reach the starting point
with car B  traveling behind by 500 meters. What should be the rate of car A and car B? traveling behind by 500 meters. What should be the rate of car A and car B?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "a" be the rate of the car A (in meters-per-minute), and
let "b" be the rate of the car B.
Then you have these two equations for two unknowns "a" and "b":
3a + 3b = 1500. (1) ("If they will start at the same point and travel opposite directions,
they will meet for the first time in 3 minutes.")
 = 1000 (2) ("But if they travel in the same direction, with the same starting point,
car A will reach the starting point with car B traveling behind by 500 meters")
Equation (1) is clear and does not require further explanation: the two cars, moving towards each other,
cover exactly one lap of 1500 meters long.
The equation (2) requires some explanations:
a) The factor = 1000 (2) ("But if they travel in the same direction, with the same starting point,
car A will reach the starting point with car B traveling behind by 500 meters")
Equation (1) is clear and does not require further explanation: the two cars, moving towards each other,
cover exactly one lap of 1500 meters long.
The equation (2) requires some explanations:
a) The factor 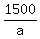 is the time for car A to reach the starting point;
b) Car B traveled that time is the time for car A to reach the starting point;
b) Car B traveled that time 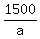 and covered only 1500 - 500 = 1000 meters.
Thus equation (2) is simply the "distance" equation D = R*T for the car B.
OK. Let us simplify equations (1) and (2):
a + b = 500 (1') ( 500 = and covered only 1500 - 500 = 1000 meters.
Thus equation (2) is simply the "distance" equation D = R*T for the car B.
OK. Let us simplify equations (1) and (2):
a + b = 500 (1') ( 500 = 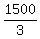 )
3b = 2a (2') ( after cross-multiplication and canceling in equation (2) )
To solve it, express a = 500 -b from (1') and substitute it into (2') to get
3b = 2(500-b) ---> 3b = 1000 - 2b ---> b = 200 m/minute
---> a = 300 m/minute. )
3b = 2a (2') ( after cross-multiplication and canceling in equation (2) )
To solve it, express a = 500 -b from (1') and substitute it into (2') to get
3b = 2(500-b) ---> 3b = 1000 - 2b ---> b = 200 m/minute
---> a = 300 m/minute.
Answer. Car A rate is 300 m/minute. Car B rate is 200 m/minute.
|
|
|