Question 1079215: 5 men are hired to complete a job. If one more man is hired, the job can be completed 8 days earlier. Assuming that all the men work at the same rate, how many more men should be hired so that the job can be completed 28 days earlier?
Found 7 solutions by josgarithmetic, Edwin McCravy, Theo, AnlytcPhil, ikleyn, greenestamps, math_tutor2020:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! The one-man rate: 1 job in 240 days
Expected time for the job with 5 men: 48 days
Number of ADDITIONAL men to do the job 28 days early: 7 men
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! The answer above and the answers below are all correct.
I like AnlytcPhil's method below best.
It takes 12 workers which is 7 more than the original 5
1 worker takes 240 days
5 workers take 240/5 = 48 days
6 workers take 240/6 = 40 days, which is 1 more worker and
8 days less, which checks.
Thus 12 workers takes 240/12 = 20 days, which is 28 days less
than the 48 days it takes 5 workers, which checks.
Edwin
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the general formula used in this type of problem is:
prt = q
p is the number of people
r is the rate at which each person works
t is the amount of time
q is the quantity of work produced.
in your problem:
t = number of days.
q = 1 job
you get:
5rt = 1
6r(t-8) = 1
the first equation says:
5 people working at a certain rate for each person for a certain amount of days = 1 job.
the second equation says:
5 people working at the same rate for each person for 8 less than a certain amount of days = 1 job.
use the first equation to solve for r in terms of t.
you get r = 1/(5t)
replace r with 1/(5t) in the second equation to get:
6 * 1/(5t) * (t-8) = 1
multiply both sides of this equation by 5t to get:
6 * (t-8) = 5t
simplify to get:
6t - 48 = 5t
subtract 5t from both sides of this equation to get:
6t - 5t = 48
solve for t to get t = 48.
your first equation of 5rt = 1 becomes 5 * r * 48 = 1
solve for r to get r = 1 / (5 * 48)
simplify to get r = 1/240
you now should know the value of the variables involved.
you have:
r = 1/240
t = 48
in the equation of 5rt = 1, you get 5 * 1/240 * 48 = 1 which results in 1 = 1 which is true.
in the equation of 6r(t-8) = 1, you get 6 * 1/240 * 40 = 1 which results in 1 = 1 which is true.
you can now solve for the number of people required to finish the job 28 days earlier.
the same equation is used.
prt = 1
r = 1/240
since t = 45, then t - 28 becomes 48 - 28 which becomes 20.
you need to solve for p
the equation of prt = 1 becomes p * 1/240 * 20 = 1
solve for p to get p = 240 / 20 = 12
you would need 12 people to finish the job 28 days earlier.
formula is prt = 1
p = 12
r = 1/240
t = 20
12 * 1/240 * 20 = 1 becomes 1 = 1 which is true.
i believe your solution will be that 12 people are required.
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
5 men are hired to complete a job. If one more man is hired, the job can be completed 8 days earlier.
Assuming that all the men work at the same rate, how many more men should be hired so that the job can be completed 28 days earlier?
~~~~~~~~~~~~~~~~~~~~~~~
Let "a" be the rate of work of one worker per day.
Then the number of days for 5 workers to complete the job is  ;
the number of days for 6 workers to complete the job is ;
the number of days for 6 workers to complete the job is  .
Thus, we can write this time equation .
Thus, we can write this time equation
 - -  = 8 days. (1)
It implies = 8 days. (1)
It implies
 - -  = 8, = 8,
 = 8,
a = = 8,
a = 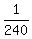 . (2)
+--------------------------------------------------------------+
| So, we found that under given condition the rate of work |
| is 1/240 of the job per day for each worker. |
+--------------------------------------------------------------+
Now we want to find the number n of additional workers (to 5 workers) to complete
the job 32 days earlier. For it, we write similar time equation to (1) . (2)
+--------------------------------------------------------------+
| So, we found that under given condition the rate of work |
| is 1/240 of the job per day for each worker. |
+--------------------------------------------------------------+
Now we want to find the number n of additional workers (to 5 workers) to complete
the job 32 days earlier. For it, we write similar time equation to (1)
 - -  = 28.
Substitute here a = 1/240, based on (2). You will get = 28.
Substitute here a = 1/240, based on (2). You will get
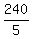 - - 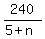 = 28.
To solve, simplify step by step. You will get
48 - = 28.
To solve, simplify step by step. You will get
48 - 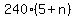 = 28,
48 - 28 = = 28,
48 - 28 = 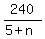 ,
20 = ,
20 = 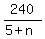 5 + n =
5 + n = 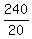 5 + n = 12.
n = 12 - 5 = 7.
+----------------------------------------------------------------+
| Second part of the solution can be worded in different way. |
+----------------------------------------------------------------+
We just found that the rate of work of one worker is 1/240 of the job per day.
It means that the entire job is 240 man-days.
5 workers can complete this job in 240/5 = 48 days.
We want the job be complete in 48-28 = 20 days.
Hence, 240/20 = 12 workers are needed, i.e. 12 - 5 = 7 workers should be added.
ANSWER. 7 workers should be hired in addition to the original 5 workers to complete the job 28 days earlier.
5 + n = 12.
n = 12 - 5 = 7.
+----------------------------------------------------------------+
| Second part of the solution can be worded in different way. |
+----------------------------------------------------------------+
We just found that the rate of work of one worker is 1/240 of the job per day.
It means that the entire job is 240 man-days.
5 workers can complete this job in 240/5 = 48 days.
We want the job be complete in 48-28 = 20 days.
Hence, 240/20 = 12 workers are needed, i.e. 12 - 5 = 7 workers should be added.
ANSWER. 7 workers should be hired in addition to the original 5 workers to complete the job 28 days earlier.
Solved.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We have two scenarios for completing the job:
(1) 5 men working for x days; and
(2) 6 men working for (x-8) days
In the first scenario, the job requires 5(x) man-days; in the second, it requires 6(x-8) days. Those amounts of time required to complete the job are the same:
5x=6(x-8)
5x=6x-48
x=48
It takes 5 men 48 days to do the job, so the number of man-days required to complete the job is 5(48) = 240.
The third scenario has the job being completed in 28 fewer days -- i.e., 48-28 = 20 days.
The job requires 240 man-days to complete; if it is to be completed in 20 days, the number of men needed is 240/20 = 12.
There are currently 5 men working on the job, so the number of additional men needed to complete the job 28 days earlier is 12-5 =7.
ANSWER: 7
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 7 extra workers
Explanation
There are many great solutions by the other tutors.
I'll offer a different viewpoint.
Consider a job of moving 9000 boxes.
I'm selecting this number since it's a multiple of 5 and 6, and because it's some large value.
It turns out that this value 9000 doesn't matter and you can pick any other value to get the same final answer at the end.
If we had 5 men working to move 9000 boxes, then each man moves 9000/5 = 1800 boxes.
Each person has a daily unit rate of 1800/x boxes per day where x is the number of days to finish the job with 5 men.
Note that: rate = (amount done)/time
Adding a 6th man will mean each person handles 9000/6 = 1500 boxes.
Each person has a unit rate of 1500/(x-8) since they complete the job 8 days early.
Assuming each man has the same unit rate, we can equate those fractions.
Solve 1800/x = 1500/(x-8) to get x = 48. I'll let the student handle the scratch work.
It will take x = 48 days if you had 5 men on the job.
The instructions state we want to finish 28 days earlier, so the timeline should be x-28 = 48-28 = 20 days.
Each worker's unit rate is 1800/x = 1800/48 = 37.5 boxes per day.
n = number of additional workers to hire in addition to the original 5 men
n+5 = number of workers total
9000/(n+5) = number of boxes each worker handles
rate*time = amount done
(37.5 boxes per day)*(20 days) = 9000/(n+5)
37.5*20 = 9000/(n+5)
I'll let the student solve that equation. You should arrive at n = 7 which is the number of extra workers you should hire so you finish 28 days early.
More practice found here
|
|
|