SOLUTION: Let x, y, and z be real numbers such that x + y + z, xy + xz + yz, and xyz are all positive. Prove that x,y, and z are all positive. Please write your solution in proof form

Algebra ->  Real-numbers -> SOLUTION: Let x, y, and z be real numbers such that x + y + z, xy + xz + yz, and xyz are all positive. Prove that x,y, and z are all positive. Please write your solution in proof form       Log On


   

Question 1078624: Let x, y, and z be real numbers such that x + y + z, xy + xz + yz, and xyz are all positive.
Prove that x,y, and z are all positive.
Please write your solution in proof form without skipping steps.
Answer by ikleyn(52802) About Me  (Show Source):
You can put this solution on YOUR website!
.
O ! it is the nice problem, and it is a pleasure to me to solve it . . . . 

Let a = x+y+z, b = xy+xz+yz and c = xyz.


We are given that all three numbers a, b and c are positive.


The Vieta's theorem says that the three numbers x, y and z are the roots of this cubical polynomial equation 

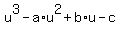u%5E3+-+a%2Au%5E2+%2B+b%2Au+-c = 0.


Now let assume that some of the numbers x, y, or z is negative.
For certainty, let's assume that "x" is negative:  x < 0.


Then, from one side, we have

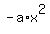x%5E3+-+a%2Ax%5E2+%2B+b%2Ax+-c = 0    (2)

(according to (1)).


From the other side, all the terms x%5E3, -a%2Ax%5E2, b%2Ax and -c are negative, and then the equality (2) is not possible.


We got a contradiction.


This contradiction means that our assumption that there is a negative root is WRONG.

Thus the statement is PROVED and the problem is SOLVED.