SOLUTION: Please help me solve this. Use determinants to find the area of the parallelogram shown at the link below. Parallelogram: https://s27.postimg.org/g9xivnbbn/figurefor16.png

    If  u = 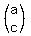  and  v =  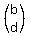 are vectors in a coordinate plane, then the area of the parallelogram which is built on these vectors 

    as on sides is equal to the modulus of the determinant,  |det 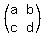|,  of the  2x2-matrix  A =  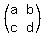 whose columns are the given vectors.

Your vector U is the vertical side of the parallelogram from the point (-1,-5) to the point (-1,1).

It has component form U = (-1-(-1),1-(-5)) = (-1+1, 1+6) = (0,7).


Your vector V is the sloped side of the parallelogram from the point (-1,-5) to the point (4,5).

It has component form V = (4-(-1),5-(-5)) = (4+1, 5+5) = (5,10).


Now make a matrix A whose columns are the components of the vectors U and V:


    A = .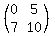


Then take its determinant  det(A) = det 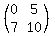 = -5*7 = -35.


Finally, take the modulus of the determinant, i.e. its absolute value.

You will get the area of your parallelogram


    S = | det (A) | = |-35| = 35.


Answer.  The area of the parallelogram is 35 square units.