Question 1078079: Hello, I would need your help with the following proof:
Let a, b, c be different prime numbers greater than 3. Show that if a + c = 2b, then 6 | (b - a).
I am really stuck with this problem, my approach would be with the theorem that every prime number > 3 divided by 6 has remainder 0 or 5.
Any help would be really appreciated!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! NOTE: In what follows, k, m, n, p, q, and r are integers.
For any pair of prime numbers a and c greater than 2,
 is an integer, is an integer,
because prime numbers greater than 2 are odd,
and the sum of two odd numbers is an even number.

(The difference of two odd numbers is also an even number).
Since  is a prime number, is a prime number,
a and c are nut just any pair of prime numbers.
They could not be 5 and 7 for example,
because  is not prime. is not prime.
Every prime number greater than 3 divided by 3 has remainder 1 or 2,
The numbers a and c divided by 3 must have the same remainder.
Otherwise, the sum would be  , ,
and since that is a multiple of 3,
b would not be a prime number, but a multiple of 3.
Not only a and c are congruent modulo 3 (they have the same remainder),
but all three primes (a, b and c) are congruent modulo 3 .
Either  , ,
or  . .
It is easy to see that the difference of two numbers congruent modulo 3
is a multiple of 3.
With r = 0, 1, or 2, that difference could be written as

So, the difference 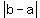 is a multiple of 3. is a multiple of 3.
It is also a multiple of 2,
because the difference of two odd numbers is even.
Since 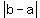 is a multiple of 3 and a multiple of 2, is a multiple of 3 and a multiple of 2,
it is a multiple of 6.
|
|
|