SOLUTION: Kim can paint the garage door in 2 hours and Jim can paint the same door in 1 hour. How long will it take them if they work together?

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Kim can paint the garage door in 2 hours and Jim can paint the same door in 1 hour. How long will it take them if they work together?      Log On


   

Question 1078031: Kim can paint the garage door in 2 hours and Jim can paint the same door in 1 hour. How long will it take them if they work together?
Found 3 solutions by josmiceli, amfagge92, Edwin McCravy:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
Kim's rate of working:
[ 1 garage door ] / [ 2 hrs ]
Jim's rate of working:
[ 1 garage door ] / [ 1 hr ]
Let +t+ = their time in hrs to paint the door
if they work together
Their rate working together:
[ 1 garage door ] / [ t hrs ]
-----------------------------
Add their rates of working to get their
rate working together
+1%2F2+%2B+1%2F1+=+1%2Ft+
Multiply both sides by +2t+
+t+%2B+2t+=+2+
+3t+=+2+
+t+=+2%2F3+ hrs
-------------------
Convert this result to minutes
+%282%2F3%29%2A60+=+40+
It will take them 40 minutes to paint the
door if they work together

Answer by amfagge92(93) About Me  (Show Source):
Answer by Edwin McCravy(20063) About Me  (Show Source):
You can put this solution on YOUR website!
Notice that the preceding answer 1.5 hrs, could not be correct because
Jim alone could paint the door in 1 hour. Surely Kim couldn't slow
Jim down that much. LOL

Kim can paint the garage door in 2 hours and Jim can paint the same door in 1 hour. How long will it take them if they work together?
You can do it with or without algebra.

Without algebra, just basic math:

If both work together for 2 hours painting garage doors
(say in a new development of houses), Kim will paint
1 garage door while Jim, the faster will paint 2 garage
doors, so together they can paint 3 garage doors in 2 
hours. So they can paint 1 garage door in 1/3 of 2 hours
which is 1/3 of 120 minutes or 40 minutes.

With algebra:

How long will it take them if they work together?
Let the answer be x hours.

Kim can paint the garage door in 2 hours.
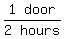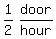
So Kim's painting rate is 1 door per 2 hours or matrix%281%2C2%2C1%2Cdoor%29%2Fmatrix%281%2C2%2C2%2Chours%29 or matrix%281%2C2%2C1%2F2%2Cdoor%2Fhour%29

Jim can paint the same door in 1 hour
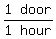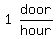So Kim's painting rate is 1 door per 1 hour or matrix%281%2C2%2C1%2Cdoor%29%2Fmatrix%281%2C2%2C1%2Chour%29 or matrix%281%2C2%2C1%2Cdoor%2Fhour%29

Together they can paint the same door in x hours:

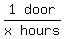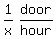So together their combined painting rate is 1 door per x hours or matrix%281%2C2%2C1%2Cdoor%29%2Fmatrix%281%2C2%2Cx%2Chours%29 or matrix%281%2C2%2C1%2Fx%2Cdoor%2Fhour%29

The equation comes from:



 

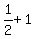
1%2F2%2B1%22%22=%22%221%2Fx

Multiply through by 2x

x%2B2x%22%22=%22%222

3x%22%22=%22%222

x%22%22=%22%222%2F3

2/3 of an hour is 2/3 of 60 minutes = 40 minutes.

Edwin