Two dice are rolled once. What is the probability that the
two numbers that show...
Here are all the possible rolls with a
red die and a green die:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
a) have a sum of 7?
There are 36 possible rolls. Now I
will underline just those which have
a sum of 7:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
There are 36 possible rolls. So
there are 6 possible rolls out of
the 36 which have that property.
Therefore the probability is 
which reduces to 
b) have a sum of at most 5?
There are 36 possible rolls. Now I
will underline just those which have
a sum of at most 5:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
There are 36 possible rolls. So
there are 10 possible rolls out of
the 36 which have that property.
Therefore the probability is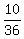 
which reduces to 
c) have a sum which is even and at least 8?
Now I will underline just those which have
a sum which is even and at least 8:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
There are 36 possible rolls. So
there are 9 possible rolls out of
the 36 which have both properties.
Therefore the probability is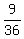 
which reduces to 
Edwin
