Question 1077821: Find all solutions of each of the equations in the interval [0,2pi).
a) sin(x+pi/3)+sin(x−pi/3)=1
b) tan(x+pi)+2sin(x+pi)=0
c) cos(x−pi/2)+sin2x=0
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) 
Using the trigonometric identities
for sine of sum an difference of two angles,
the equation can be re-written as
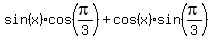  
Taking out  and and  as common factors as common factors
the equation can be re-written as
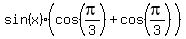  
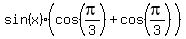  

We know that  , so we re-write the equation as , so we re-write the equation as
 and and  . .
In the interval [0,2pi), that happens only for
 . .

b) 
Based on trigonometric identities, the equation can be re-written as
 and and  . .
Then, with some algebra, it can be re-written as
 and and 
The numerator is zero when
 ---> --->  or or  . .
The numerator is also zero when
 ---> --->  ---> --->  or or  . .
For none of those values of x, is the  zero, zero,
so they are all valid solutions.

c) 
(Or did you mean  instead?) instead?)
Using trigonometric identities,
the equation can be re-written as
 <--> <-->  and and  . .
If the second term was really  , ,
using the trig identity for double angles,
the equation can be re-written as
 <---> <---> 
The expression 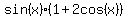 is zero when is zero when
 ---> --->  or or  . .
The expression 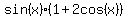 is also zero when is also zero when
 <---> <--->  . .
In the interval [0,2pi), that happens for
 or or  . .

NOTE: For  , ,
 <--> <-->  , ,
in the interval [0,2pi) has solutions when
 --> -->  or or  , ,
and when
 --> -->  --> -->  . .
|
|
|