Question 1077791: Bob was standing in front of tall building. As he moves 75 feet closer to the building, his angle of elevation changes from 20 degree to 35 degree. What is the height of this building?
Please help me to solve this. Thanks.
Found 3 solutions by Boreal, josgarithmetic, MathTherapy:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! It helps to draw this.
If x is the number of feet to the building, and y is the height of the building.
tan 20=y/x
tan 35=y/(x-75)
y=(x-75)*0.7002=0.7002x-52.515
y=0.3640x
therefore, 0.3640x=0.7002x-52.515
so 52.515=0.3362x
x=156.20 feet
y=x tan 20=56.853 feet tall--building.
check with the other, 81.20 feet from the building.
y=81.20*tan 35=56.856 feet
round to 56.9 feet tall.
Answer by josgarithmetic(39621)  (Show Source):
You can put this solution on YOUR website! Two right triangles.
When at 20 degree elevation, angle of depression 55 degree; distance from building x+75.
When at 35 degree elevation, angle of depression 70 degree; distance from building, x.
y, height of building.
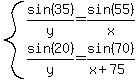
Solve for y.
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website!
Bob was standing in front of tall building. As he moves 75 feet closer to the building, his angle of elevation changes from 20 degree to 35 degree. What is the height of this building?
Please help me to solve this. Thanks.
1) Use distance he traveled to get closer (75'), the original angle of elevation (20o), the difference between the angles of elevation 15o (35o - 20o),
and the law of sines to get the length of the hypotenuse of the triangle, formed from his current distance from the building and the height of the building.
This should be: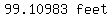 
2) Use the length of the hypotenuse above (99.10983 feet), along with the 35o ∠, and the SINE ratio to get the height of the building.
This should be: 
|
|
|
