Question 1077717: A circular point P(a,b) moves clockwise around the circumference of a unit circle starting at (1,0) and stops after covering a distance of 8.305 units. Find the coordinates of where P stops (round to three decimal places) and what quadrant it lies in.
Can someone help me with this?
Thank you.
Found 2 solutions by ikleyn, KMST:
Answer by ikleyn(52914)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  (corrected based on misreading pointed out by ikleyn) (corrected based on misreading pointed out by ikleyn)
Thanks ikleyn.
The point traveled  8.305 times the radius, and the radius of the unit circle is 1. 8.305 times the radius, and the radius of the unit circle is 1.
That means the point swept and angle of 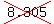 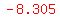 radians . radians .
Its coordinates are
  , and , and
 
  . .
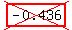
Those coordinates tell you the point is in quadrant  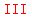 , ,
because x is negative and y is 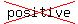 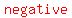 . .
For another point of view:
Since  is one turn is one turn  around the circle, around the circle,
the point is now  radians into its second lap around the circle. radians into its second lap around the circle.
That is less than half a turn, which would be  radians, radians,
so it has to be in quadrant  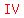 or or 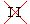 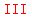 . .
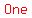     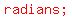
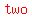  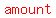   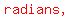
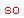  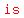 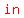 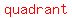 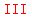 . .
You could also divide 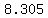 by by 
to see that the point covered 5 whole quadrants,
and part of a 6th quadrant,
so with the first 4 quadrants being one whole turn,
started a second lap, and it is now in the second quadrant
     . .
    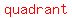 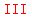 . .
|
|
|