Question 1077651: can someone please determine value of variable for which expansion is defined as a real number
square root(x^2-5x-50)?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your equation is y = sqrt(x^2 - 5x - 50)
in order for the value of y to be real, x^2 - 5x - 50 must be greater than or equal to 0.
if you set x^2 - 5x - 50 equal to 0, you will find that the factors are (x-10) * (x+5) = 0
therefore x^2 - 5x - 50 is equal to 0 when x = 10 and when x = -5.
you need to look at the interval from minus infinity to -5; from -5 to 10, from 10 to plus infinity to see where the value of the function lies.
since the coefficient of the x^2 term is positive, than the quadratic equation points down and opens up.
this means the interval from minus infinity to -5 is positive or 0, and the interval from 10 to plus infinity is positive or 0, and the interval between -5 and 10, not including -5 and 10, isnegative.
what this says is that x^2 - 5x - 50 is negative when -5 < x < 10.
otherwise, it is positive or 0.
therefore sqrt(x^2 - 5x - 50) is not real when -5 < x < 10 and is real otherwise.
this is because the sqrt of a number can't be negative if you want the solution to be real.
if you graph the equation of y = x^2 - 5x - 50, it will look like this:
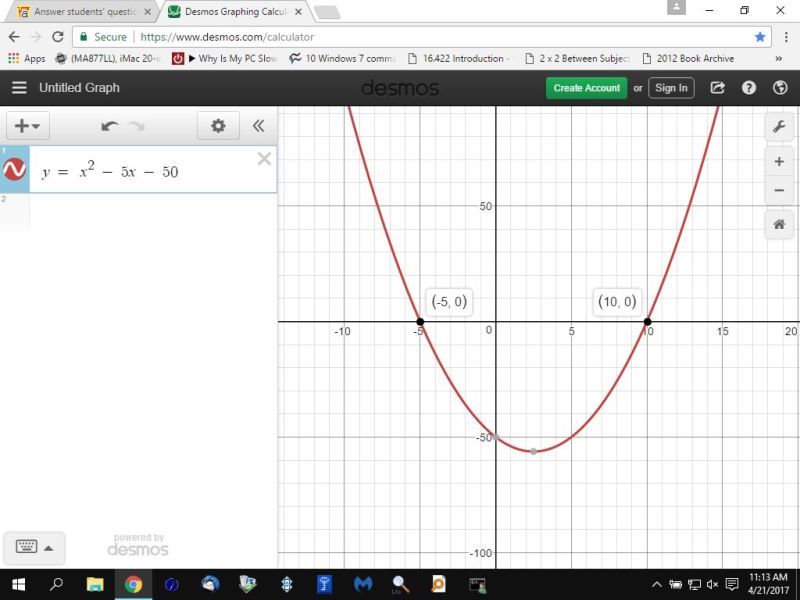
if you graph the equation of y = sqrt(x^2 - 5x - 50, it will look like this:
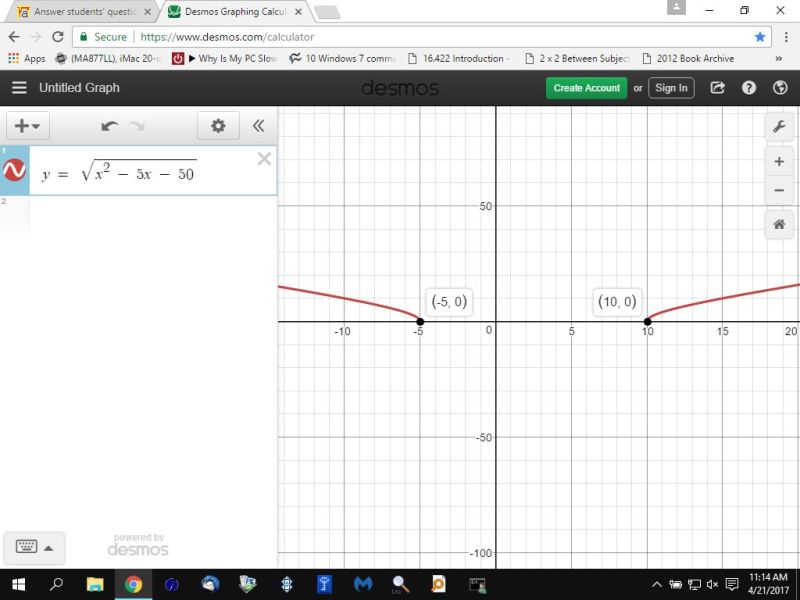
the graph of sqrt(x^2 - 5x - 50) will be blank in the interval of -5 < x < 10 because the square root is negative in that interval which is not a real number and therefore can't be graphed in the real number plane.
|
|
|