SOLUTION: Below is what I have so far: A basketball team sells tickets that cost $10, $20, or, for VIP seats, $30. The team has sold 3343 tickets overall. It has sold 113 more $20 tickets

Algebra ->  Finance -> SOLUTION: Below is what I have so far: A basketball team sells tickets that cost $10, $20, or, for VIP seats, $30. The team has sold 3343 tickets overall. It has sold 113 more $20 tickets      Log On


   

Question 1077631: Below is what I have so far:
A basketball team sells tickets that cost $10, $20, or, for VIP seats, $30. The team has sold 3343 tickets overall. It has sold 113 more $20 tickets than $10 tickets. The total sales for $62,350. How many tickets have been sold?
How many $10 tickets were sold?
How many $20 tickets were sold?
How many $30 tickets were sold?
I have been able to figure out:
3343 tickets overall
113 more $20 tickets than $10 tickets
62,350 total sales
$10 = a
$20 = b
$30 = c
a + b + c = 3343
b = a + 113
10a + 20b + 30c = 62350
This is where I am stuck:
a+2b+3c= (should this be 140)?
What do I need to do from here, specifically, in order to get the three ticket sold amounts? Please be specific in your steps.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
10a%2B20b%2B30c=62350

%281%2F10%29%2810a%2B20b%2B30c%29=%281%2F10%29%2862350%29

a%2B2b%2B3c=6235

-

You could change your second equation to a=b-113.

System is now system%28a%2Bb%2Bc=cross%283433%293343%2Ca=b-113%2Ca%2B2b%2B3c=6235%29.

--
You can use the second equation to substitute for a.
system%28%28b-113%29%2Bb%2Bc=cross%283433%293343%2C%28b-113%29%2B2b%2B3c=6235%29

and simplify,

system%282b%2Bc=3456%2C3b%2B3c=6348%29

system%282b%2Bc=3456%2Cb%2Bc=2116%29--------simpler system in the variables b and c. You could try elimination, of at least c to quickly find b.,
...


-
system%28b=1340%2Cc=776%2Ca=1227%29

Answer by MathTherapy(10557) About Me  (Show Source):
You can put this solution on YOUR website!
Below is what I have so far:
A basketball team sells tickets that cost $10, $20, or, for VIP seats, $30. The team has sold 3343 tickets overall. It has sold 113 more $20 tickets than $10 tickets. The total sales for $62,350. How many tickets have been sold?
How many $10 tickets were sold?
How many $20 tickets were sold?
How many $30 tickets were sold?
I have been able to figure out:
3343 tickets overall
113 more $20 tickets than $10 tickets
62,350 total sales
$10 = a
$20 = b
$30 = c
a + b + c = 3343
b = a + 113
10a + 20b + 30c = 62350
This is where I am stuck:
a+2b+3c= (should this be 140)?
What do I need to do from here, specifically, in order to get the three ticket sold amounts? Please be specific in your steps.
No!! 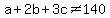a+%2B+2b+%2B+3c+%3C%3E+140 

$10 = a

$20 = b

$30 = c



a + b + c = 3,343 ------ eq (i)

b = a + 113 ------- eq (ii)

10a + 20b + 30c = 62,350______10(a + 2b + 3c) = 10(6,235)_____a + 2b + 3c = 6,235 ------- eq (iii)

a + a + 113 + c = 3,343 ------- Substituting a + 113 for b in eq (i)

2a + c = 3,230 ------ eq (iv)



a + 2(a + 113) + 3c = 6,235 ------- Substituting a + 113 for b in eq (iii)

a + 2a + 226 + 3c = 6,235 

3a + 3c = 6,009 ------ eq (v)

- 6a - 3c = - 9,690 ----- Multiplying eq (iv) by - 3 ------ eq (vi)

- 3a = - 3,681------ Adding eq (vi) & (v)



You should now be able to find the number of $20 and $30 tickets sold!!

Word of advice: STAY away from ANY and EVERYTHING that the other person tells you to do. You will never, in a million years,

                find the correct answer if you so choose to not heed my warning!