SOLUTION: In right triangle ΔABC (m∠C = 90°), point P is the intersection of the angle bisectors of the acute angles. The distance from P to the hypotenuse is equal to 4 in. Fin

  

  

The drawing to the problem is shown in the Figure to the right.
The angle bisectors are shown in green.

The intersection of angle bisectors is a remarkable point in ANY triangle. NAMELY, 
it is the center of the inscribed circle and is equidistant from the sides of a triangle.         


    (By the way, the third angle bisector goes through the same intersection point, 
    since in any triangle the angle bisectors are concurrent.

    See the lesson Angle bisectors of a triangle are concurrent in this site).

Since the condition says that the distance from the point P to the hypotenuse is equal to 4,
it means that the radius of the inscribed circle is equal to 4 inches.

The inscribed circle with the center at the point P is shown in red in the Figure.

Also, the radii PQ, PR and PS are drawn (in blue) from the center to the tangent points.
 
  




 
 
Due to well known property, the radii are perpendicular to the tangent segments, i.e. to the sides of the triangle.

Now, let x be the length of the segment AQ from the vertex A to the tangent point Q, in inches.
Then the length of AS is also equal to x inches.
Then the length of BS is equal to (20-x) inches.
Then the length of BR is equal to (20-x) inches.

It implies that the leg AC of the triangle ABC is (x+4) inches long, while the leg BC is (20-x+4) = (24-x) inches long.

Then we have the Pythagorean equation to find x

 = .

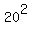After simplifications, it reduces to 

 = 

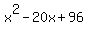and is solved by factorization

(x-12)*(x-8) = 0.

The roots are x= 12 and x= 8.

It gives for the legs of the triangle ABC their lengths (16,12) or (12,16).